Halvmåner

Stikkord: Areal Pytagoras Bevis

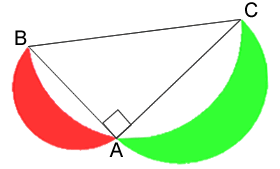
Trekanten ABC er rettvinklet, vinkel A er rett. Det er tegnet en halvsirkel på hver av sidene i trekanten. Da dannes det to «månesigder», slik de fargelagte områdene på figuren viser.

Kan du vise at arealet av de to månesigdene tilsammen er lik arealet av trekanten?

• Du trenger ikke en gang å regne ut arealene for å bevise påstanden.

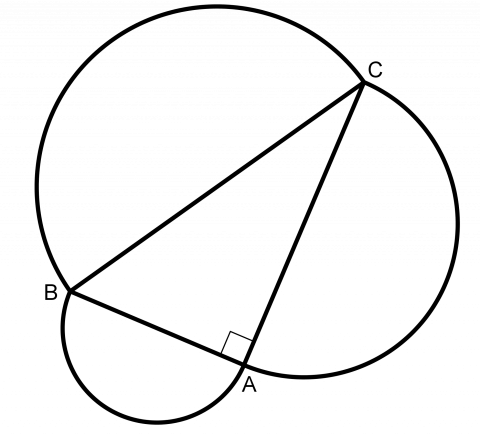
Vi kan starte med å la halvsirkelen på hypotenusen vende den andre veien.

Ved Pytagoras’ setning kan vi vise at

Areal halvsirkel på AB + areal halvsirkel på AC = Areal halvsirkel på BC

Areal halvsirkel på BC:

$\frac12 \pi \left(\frac{BC}{2}\right)^2=\frac{\pi}{8} (BC)^2$

Areal halvsirkler på de to katetene:

$\frac12 \pi \left(\frac{AB}{2}\right)^2+\frac12 \pi \left(\frac{AC}{2}\right)^2\\ =\frac{\pi}{8} \left((AB)^2+(AC)^2\right)\\ =\frac{\pi}{8} (BC)^2\\$

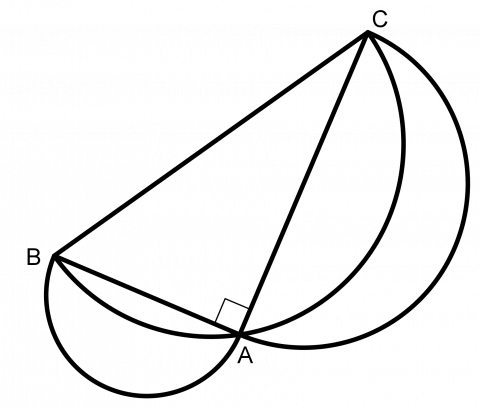
Når vi lar halvsirkelen på hypotenusen vende inn over trekanten, vil toppunktet i den rette vinkelen, A, ligge på sirkelbuen. Så det vil alltid dannes to månesigder, uansett form på den rettvinklede trekanten.

Halvmåner som er dannet utenfor en trekant

Når halvsirkelen på hypotenusen vender innover i figuren ser vi at vi kan uttrykke arealet av de to månesigdene som

Areal trekant ABC + (areal halvsirkel på AB + areal halvsirkel på AC) – areal halvsirkel på BC

= areal trekant ABC

Ressursen er utviklet av NRICH

Halvmåner

Aktivitet

Starthjelp

Løsning