Tetraederproblemer
Aktivitet
Er det mulig å lage et tetraeder der lengdene av de seks sidekantene er 10, 20, 30, 40, 50 og 60 lengdeenheter?
Er det mulig at et tetraeder kan ha sidekanter med lengder 10, 20, 25, 45, 50 og 60 enheter?
Kan du lage generelle regler som vi kan bruke for å sjekke om 6 gitte lengder kan være sidekanter i et tetraeder?
Starthjelp
• Du kan kutte opp sugerør og tre tråder igjennom for å eksperimentere med ulike sidelengder.
• Eller du kan klippe ut trekanter i stivt papir og prøve om de kan settes sammen til et tetraeder.
Løsning
Det kan ikke lages noe tetraeder med sidelengder på 10, 20, 30, 40, 50 og 60 enheter. Ingen av trekantene som kan lages, kan ha en sidelengde på 10 enheter, for i alle trekanter må to sider til sammen være lengre enn den tredje (trekantulikheten). Hvis vi for eksempel prøver å lage en trekant med sidelengder 10, 20 og 30, blir trekanten en rett linje.
Men vi kan lage et tetraeder med sidelengder på 10, 20, 25, 45, 50 og 60 enheter. Vi kan ha fire trekanter med sidelengder
25, 50, 60 for 25 + 50 > 60 , 25 + 60 > 50 og 50 + 60 > 20
10, 20, 25 for 10 + 20 > 25, 10 + 25 > 20 og 20 + 25 > 10
10, 45, 50 for 10 + 45 > 50, 10 + 50 > 45 og 45 + 50 > 10
20, 45, 60 for 20 + 45 > 60, 20 + 60 > 45 og 45 + 60 > 20
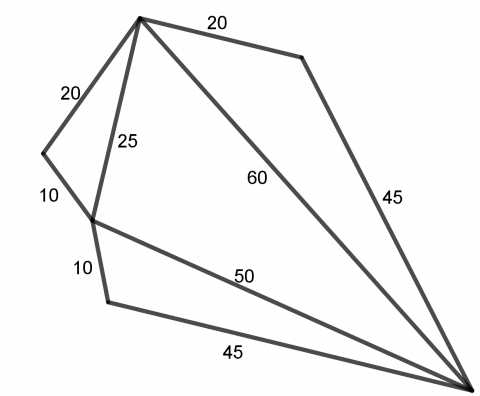
Vi kan tenke oss tetraederet ser slik ut hvis vi bretter det ut:
Kravet er altså at vi må kunne sette sammen sidelengdene til fire trekanter som alle oppfyller kravene til ulikheter, slik det er vist ovenfor. Det er egentlig tilstrekkelig at de to korteste sidene i trekanten til sammen er lengre enn den lengste siden.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Dette problemet er en fin anledning til å bruke og visualisere en idé som de kjenner fra 2D-geometri i 3D. Elevene må tenke nøye igjennom alle hensyn de må ta, og hvordan de skal arbeide, slik at de er sikre på å ha prøvd ut alle mulige kombinasjoner.
Mulig tilnærming
Du kan skrive ut oppgaven fra denne kopioriginalen.
Skriv tre tall på tavla, og tegn nøyaktig en trekant med disse tre sidelengdene. Du kan for eksempel bruke GeoGebra eller et lignende verktøy til det.
Gjør det samme på nytt med tre andre lengder.
Skriv så opp tre nye lengder, men i stedet for å tegne skriver du bare et spørsmålstegn. Etter litt tenketid kan en elev komme og tegne trekanten.
Sett til slutt opp tre lengder som ikke vil gi en trekant, etterfulgt av et spørsmålstegn. Når elevene ser at dette er umulig, kan dere snakke sammen om det i klassen. Hvorfor kan ikke dette være sidelengder i en trekant? Kan vi formulere en regel? Sørg for at dere kommer fram til trekantulikheten, med ord eller symboler (eller begge deler).
Nå kan klassen få problemet i dette opplegget.
La elevene arbeide parvis eller i små grupper. Det gjelder å finne en systematisk måte å gå fram på for å være sikker på at en har sjekket alle muligheter for trekanter, og at en ikke har oversett noen trekant som er umulig.
Til slutt må dere trekke sammen trådene og sørge for at alle får den riktige løsningen, og at de ser hvordan kravene er oppfylt. Alle trekantene må oppfylle trekantulikheten, og sammenfallende sider i to trekanter må ha samme lengde. Dessuten må alle de seks lengdene i oppgaven være tatt i bruk.
Gode veiledningsspørsmål
• Hvordan vet du at du har prøvd alle mulige kombinasjoner?
• Er det mulig å konstruere mer enn ett tetraeder?
Mulig utvidelse
Kan du finne seks lengder som kan gi mer enn ett tetraeder?
Mulig støtte
Aktiviteten Konstruer trekanter! gir elevene erfaringer med trekantulikheten. Hvilke lengder kan danne trekanter, og hvilke kan ikke?
Ressursen er utviklet av NRICH