Overlappende bånd
Problem
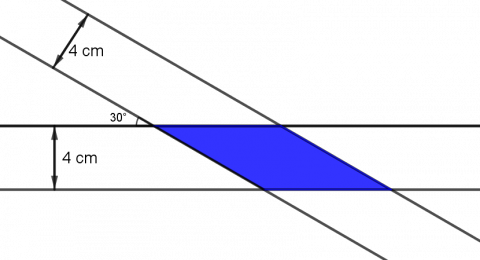
To bånd som begge er 4 cm brede, legges over hverandre slik at de danner en vinkel på 30o med hverandre, slik figuren viser.
Finn den eksakte størrelsen av området der de overlapper, dvs. det blå området på figuren.
Løsning
Løsning ved å finne arealet av et parallellogram
Det blå området er et parallellogram.
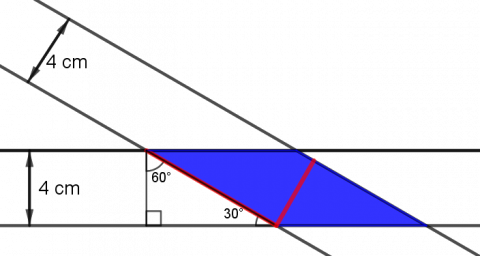
To linjestykker er markert med rødt:
Grunnlinja i parallellogrammet er \(8\:\rm{cm}\), for den er hypotenus i en rettvinklet trekant med vinkler \(30^\circ\) og \(60^\circ\), der den korteste kateten er \(4\:\rm{cm}\).
Høyden i parallellogrammet er bredden på båndene, \(4\:\rm{cm}\).
Parallellogrammets areal er \(8\:\rm{cm} \cdot 4\:\rm{cm} = 32\:\rm{cm}^2\).
Løsning ved å finne areal av trekanter
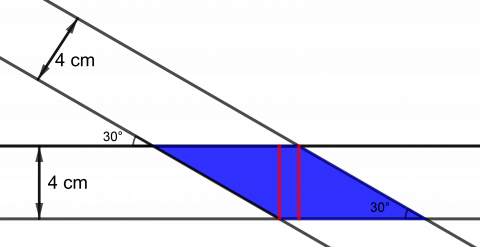
Vi kan tegne to linjer som står vinkelrett på kantene av det ene båndet, slik figuren viser. Vi får to like store rettvinklede trekanter og et rektangel.
Den korte kateten i trekantene er \(4\:\rm{cm}\) lang, og hypotenusen er \(8\:\rm{cm}\), siden de spisse vinklene i trekanten er \(30^\circ\) og \(60^\circ\). Vi regner ut den lengste kateten:
\(\sqrt {8^2-4^2}=\sqrt{64-16}=\sqrt{48}=\sqrt{16\cdot3}=4\sqrt3\)
Areal av en trekant er
\(\frac12 \cdot 4 \cdot 4\sqrt3 =8\sqrt3\)
Den korte siden i rektangelet er \(8-4\sqrt3\), og arealet av rektangelet blir da \((8-4\sqrt3)\cdot4=32-16\sqrt3\)
Til sammen blir arealet av to trekanter og et rektangel \(2\cdot 8\sqrt3 + 32-16\sqrt3=32\)
Arealet av det overlappende området er \(32\:\rm{cm}^2\).
Ressursen er utviklet av NRICH