Båten skal til land
Problem
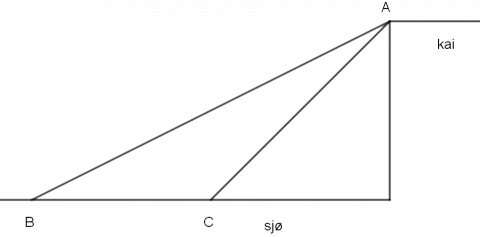
Tenk deg at du trekker en båt inn mot en kai, slik figuren viser.
Du kjører 1 m innover på kaia. Vil båten da ha flyttet seg mer enn 1 meter, mindre enn 1 meter eller nøyaktig 1 meter?
Løsning
Løsning ved å bruke Pytagoras’ setning
Figuren illustrerer situasjonen før og etter at båten har blitt flyttet fra posisjon B til posisjon C. Den har beveget seg distansen BC.
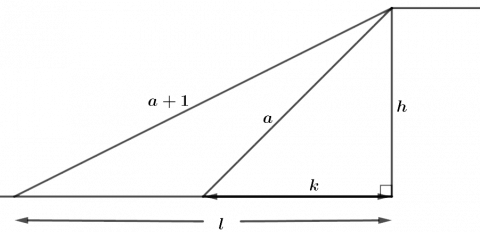
I figur 3 er sidene i de to rettvinklede trekantene markert.
Vi bruker Pytagoras’ setning:
\(l^2 + h^2 = (a + 1)^2\\ l^2+ h^2=a^2 + 2a +1\)
og
\(h^2+k^2=a^2\)
Vi trekker de to likningene fra hverandre og får
\(l^2-k^2= 2a+1\), så
\(l^2 = k^2+2a+1\)
Hvis båten hadde flyttet seg 1 m, ville \( l=k+1\) og dermed \(l^2=(k+1)^2=k^2+2k+1\)
Men a er hypotenus, og k er katet i en rettvinklet trekant, så a > k, og \(k^2+2a+1>k^2+2k+1\)
Da er \(l^2>k^2+2k+1 \implies l>k+1\)
Det vil si at båten har beveget seg mer enn 1 meter.
Løsning ved tegning og trekantulikheten
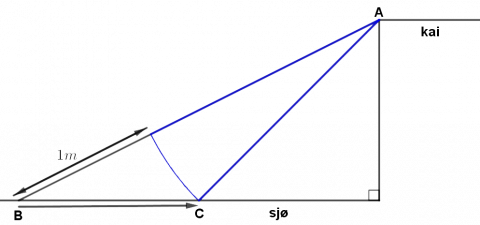
Båten har beveget seg fra B til C.
Lengden AC har blitt rotert rundt A slik at de to blå linjestykkene har samme lengde.
Tenk deg at du beveger deg fra B til A. Det vil være lenger å bevege seg strekningen BC + AC enn å bevege seg langs BA. Da må BC > 1 m. Altså vil båten bevege seg mer enn 1 m.
Ressursen er utviklet av NRICH