Overlappende kvadrater
Problem
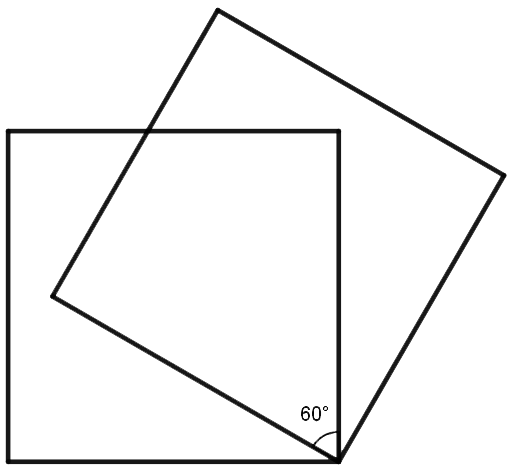
To kvadrater med sidelengde 2 er lagt over hverandre slik at det dannes en vinkel på 60o mellom dem, som figuren viser.
Hvor stort er arealet av området der de overlapper hverandre?
Løsning
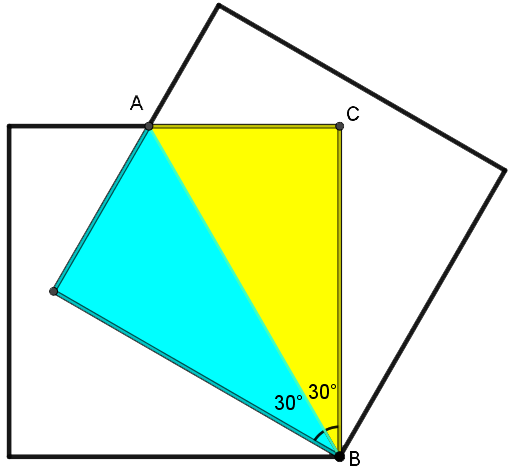
Løsning ved å dele området i rettvinklede trekanter
I trekanten \(ABC\) er \(BC = 2\). Vi kan finne \(AC\):
\(tan\:30^\circ = \frac{1}{\sqrt3}\\ tan\:\angle ABC= \frac{AC}{BC} = \frac{AC}{2}\\ \frac{AC}{2} = \frac{1}{\sqrt3}\\ AC=\frac{2}{\sqrt 3}\)
Arealet av trekanten ABC er
\(\frac12 \cdot BC \cdot AC= \frac12 \cdot 2\cdot \frac {2}{\sqrt3} = \frac {2}{\sqrt3}\)
Arealet av hele overlappingen er det dobbelte:
\(2 \cdot \frac{2}{\sqrt3}= \frac{4}{\sqrt3}\\ \frac{4}{\sqrt3} \approx 2,31\)
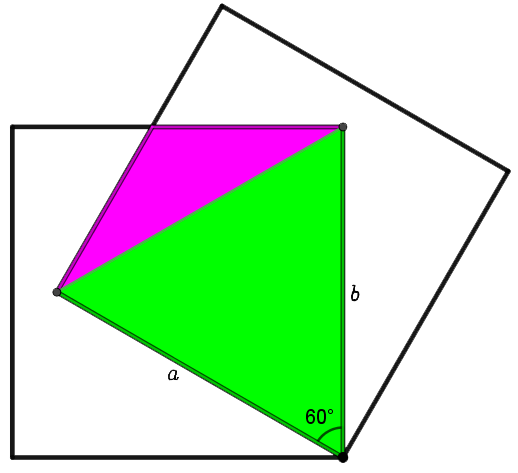
Løsning ved å dele overlappingen inn i trekanter
Vi bruker arealformelen på den grønne trekanten:
\(A=\frac12 ab \cdot sin60^\circ=\frac12 \cdot2\cdot2\cdot\frac{\sqrt3}{2}=\sqrt3\\ \sqrt3 \approx 1,73\)
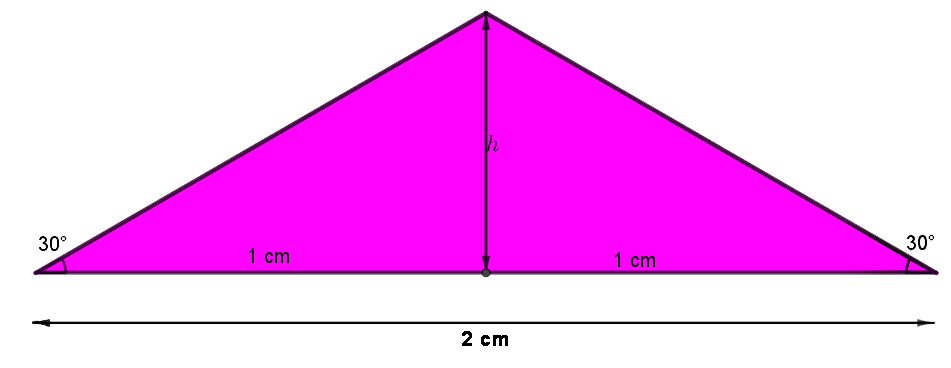
Siden den grønne trekanten er likebeint og har en vinkel på \(60^\circ\), må de to øvrige vinklene også være \(60^\circ\). Siden som den grønne og den rosa trekanten har felles, er \(2\) cm lang. Dessuten må de to spisse vinklene i den rosa trekanten være \(30^\circ\). (Hvorfor?)
\(tan 30^\circ = \frac {h}1=h= \frac{1}{\sqrt3}\)
Areal av den rosa trekanten er
\(\frac12\cdot2 \cdot \frac{1}{\sqrt3} =\frac{1}{\sqrt3} \approx0,58\)
Arealet av hele overlappingen er da
\(1,73 + 0,58 = 2,31\)
Ressursen er utviklet av NRICH