Geometrisk trigonometri
Problem
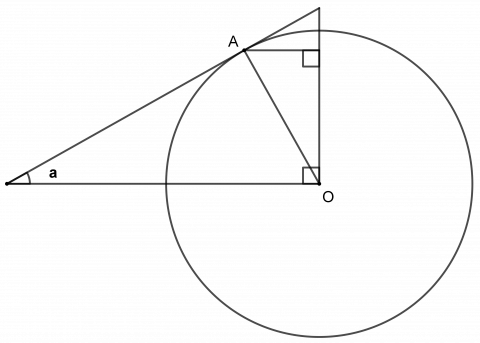
På figuren er OA radius i en enhetssirkelEnhetssirkelen er en sirkel der radien er 1 og omkretsen er 2π. Det er vanlig å sette sirkelen i et koordinatsystem, med sentrum i origo. (r = 1). Hypotenusen i den store trekanten tangerer sirkelen i A.
Finn disse lengdene i figuren:
\(\cos a, \sin a, \tan a, \frac {1}{\cos a},\frac{1}{\sin a}, \frac {1}{\tan a}\)
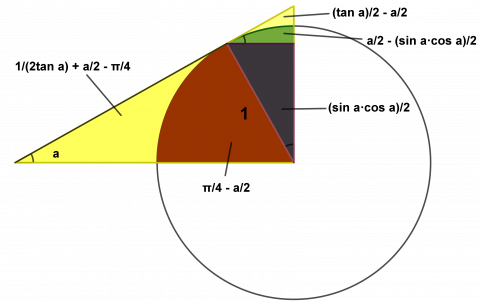
Finn arealene til alle områdene figuren er delt opp i.
|
Visste du at … Mens trigonometriske funksjoner er definert algebraisk i mer avanserte presentasjoner, kan geometriske bilder som dette gi stor innsikt i sammenhengen mellom funksjonene. Vi kan også se litt av skjønnheten og den indre sammenhengen i matematikken, noe som inspirerer mange matematikkelever. |
Løsning
Dette er som et puslespill, og det er mange måter å løse oppgaven på.
For å regne ut alle lengdene har vi brukt følgende metode:
- Marker alle rette vinkler (husk at i en sirkel vil en tangent og radien til tangeringspunktet stå vinkelrett på hverandre).
- Marker vinkel a alle steder der den forekommer (rødt på figuren).
- Marker enhetslengden (radien).
For å finne lengdene som er lik sin a, cos a og tan a, ser vi på en trekant som har en katet eller hypotenus med lengde 1. For å finne de tre øvrige lengdene må vi bruke formlikhet mellom to trekanter. Ved å sette opp forholdet mellom to og to samsvarende sider finner vi \(\frac {1}{\cos a},\frac{1}{\sin a}, \frac {1}{\tan a}\).
For å finne alle arealene må vi bestemme hvilken måleenhet vi skal bruke på vinkel a. Vi velger radianer: Det er 2π radianer i en sirkel. Vi vil bruke formlene for areal av sirkel og trekant.
Ressursen er utviklet av NRICH