Firkant i firkant
Aktivitet
I denne oppgaven kan det være nyttig å bruke prikkarket som du finner her.
Tegn en konveks firkant. (En konveks firkant har bare vinkler som er mindre enn 180˚.)
Marker midtpunktene på alle sidene, og tegn en firkant mellom midtpunktene.
Tegn noen flere konvekse firkanter, og tegn firkanter inne i dem på samme måte.
Hva legger du merke til med de nye firkantene som du tegnet inne i de første du tegnet?
Skjer det samme i alle tegningene?
Kan du finne noe mot-eksempel?
Kan du formulere en påstand som du mener alltid vil være sann?
Du kan utforske påstanden med denne GeoGebra-appleten:
Kan du bevise at påstanden din er sann?
Utgjør arealet av firkanten PQRS alltid samme andel av arealet av firkanten ABCD?
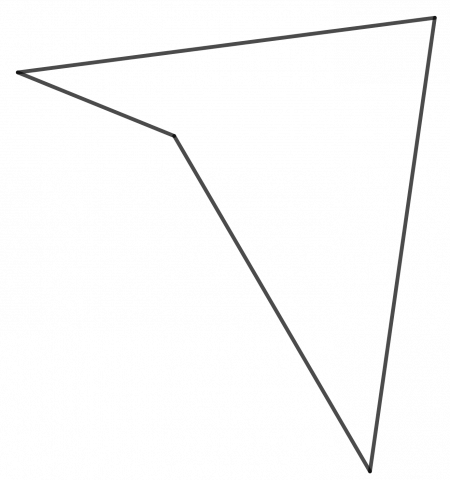
Hva hvis ABCD er en konkav firkant?
Et eksempel på en konkav firkant:
Starthjelp
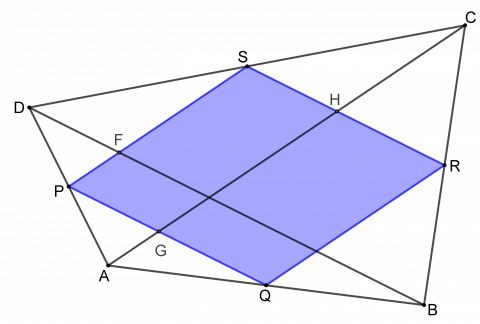
I denne figuren er diagonalene AC og BD tegnet inn.
- Hva kan du si om linjene AC og PS?
- Kan du bevise det?
Løsning
- Firkanten som tegnes mellom midtpunktene på sidene inne i en hvilken som helst firkant, er et parallellogram.
- Arealet av parallellogrammet er alltid halvparten av arealet av firkanten vi tegner først.
Dette kan vises på flere måter, her er en av dem:
1.
ΔACD og ΔPSD er formlike fordi de har vinkel ADC felles, og forholdene DC : DS = 2 : 1 og DA : DP = 2 : 1.
Da er PS || AC.
På tilsvarende måte kan vi betrakte ΔACB og ΔQRB og vise at QR || AC.
Siden PS || AC og QR || AC, må PS || QR.
På tilsvarende måte kan vi vise at PQ || SR.
Da har vi vist at firkanten PQRS er et parallellogram, uansett hvilken form firkant ABCD har.
2.
Siden forholdet mellom sidene i trekantene ΔACD og ΔPSD er 2 : 1, er forholdet mellom arealene av de samme to trekantene 4 : 1. Altså er arealet av ΔPSD \(\frac{1}{4}\) av arealet til ΔACD.
ΔPFD og ΔAGP er kongruente fordi de har like lange sider og like store vinkler (siden PQRS er et parallellogram). Tilsvarende er også ΔHCS og ΔFSD kongruente. Arealet av ΔAGP og ΔHCS er altså til sammen lik arealet av ΔPSD. De hvite trekantene som ligger inne i ΔACD, utgjør dermed halve arealet av trekanten. Da må firkanten GHSP utgjøre halve arealet av ΔACD.
På tilsvarende måte kan vi vise at arealet av den fargede firkanten GQRH, som ligger inne i ΔABC, har halvparten så stort areal som ΔABC.
Da må det fargede parallellogrammet ha halvparten så stort areal som firkanten ABCD.
Ekstra:
Det samme som gjelder konvekse firkanter, vil gjelde om firkanten er konkav.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Dette problemet inviterer elevene til å oppdage et overraskende resultat som er sant for alle firkanter, selv om vi begynner med å be dem undersøke konvekse firkanter. GeoGebra-appleten gjør det raskt å se mange eksempler. Elevene vil kunne oppdage at de kan dra i hjørnene i alle retninger, og hele tiden ser det ut til at den fargede firkanten er et parallellogram. Og de ser arealene av de to firkantene, så det skal være lett å gjette på en sammenheng mellom dem. Da blir beviset den viktigste utfordringen.
Mulig tilnærming
Du kan begynne med å la elevene tegne ulike firkanter på prikkpapir som kan skrives ut herfra. Be dem markere midtpunktene på alle sidene i firkantene, og tegne firkanter mellom disse punktene inne i hver firkant. Så snart de er ferdige med et par eksempler, kan du høre om noen har merket seg noe spesielt i tegningene. Dette er en god anledning til å diskutere ut fra eksemplene de har valgt. Har de tegnet firkanter som har spesielle symmetrier som kan ha påvirket det de har funnet ut? Hva må en ta hensyn til for at eksemplene skal gjelde for alle mulige firkanter?
Når dere har kommet så langt, kan elevene få utforske flere firkanter i GeoGebra-appleten under Aktivitet, eller de kan tegne selv i GeoGebra.
Det å tegne inn diagonalene i den ytre trekanten kan være til god hjelp når de skal prøve å bevise det de mener å ha observert.
Så kan de studere formen til den indre firkanten og lete etter en sammenheng mellom arealene av de to firkantene.
Gode veiledningsspørsmål
- Hva er spesielt med firkanten du får når du tegner linjer mellom midtpunktene på sidene?
- Vil firkanten mellom midtpunktene forandre form hvis du tar utgangspunkt i firkanter med forskjellig form?
- Kan det være en hjelp å tegne diagonalene i den ytre firkanten?
- Finnes det kongruente figurer i tegningen?
- Kan det hjelpe deg til å finne forholdet mellom arealene?
Mulig utvidelse
Hva skjer hvis du begynner med en konkav firkant?
Mulig støtte
Elevene kan begynne med å undersøke hva som skjer hvis de forbinder midtpunktene på sidene i en trekant, slik at de får en ny trekant inni den første.
Ressursen er utviklet av NRICH