Symmetriske vinkler

Stikkord: Lengder Areal Vinkler

Problem

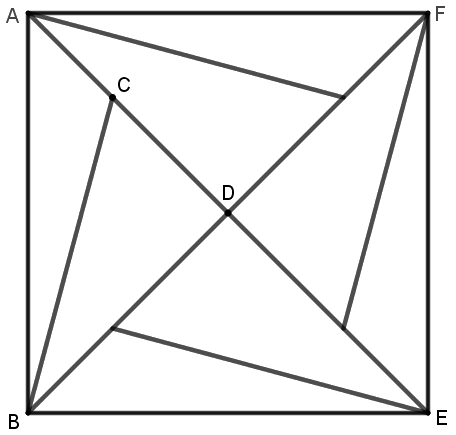
Trekanger i en firkant

Figuren har rotasjonssymmetri av orden 4 om punkt D (en figur med rotasjonssymmetri av orden 4 vil gjenta seg selv fire ganger i løpet av en rotasjon på 360˚).

Vinkel ABC er 15o, og arealet av ABEF er 24 cm2.

Hvor langt er linjestykket CD?

Løsning

At figuren har rotasjonssymmetri av orden 4 om \(D\), betyr at \(ABEF \) er et kvadrat.

Arealet av \(ABEF = 4\cdot\triangle BDA=4\cdot \frac12 BD\cdot DA= 2\cdot (BD)^2=24 \:\rm{cm}^2\), så da er

\(BD=\sqrt{12} \:\rm{cm}=2 \sqrt3\:\rm {cm}\).

Siden \(ABEF\) er et kvadrat, er \(\angle ABD = 45^\circ\) og dermed \(\angle CBD=45^\circ-15^\circ = 30^\circ\)

\(\tan 30^\circ = \frac{CD}{BD}=\frac{CD}{2\sqrt3}\ \Rightarrow CD=2\sqrt3\cdot \tan 30^\circ \:\rm{cm}=2 \sqrt3 \cdot \frac{1}{\sqrt3}cm=2\:\rm{cm}.\\ CD = 2 \:\rm{cm}.\)

Ressursen er utviklet av NRICH

10