Bøyde arealer
Aktivitet
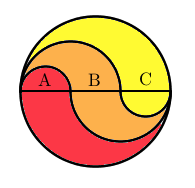
Se på denne figuren:
Kan du se hvordan denne figuren er tegnet?
Prøv å tegne en slik figur bare ved hjelp av passer og linjal.
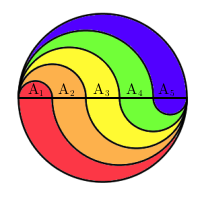
Her er det to figurer til som er tegnet på tilsvarende måte:
|
|
|
Finn ut hvor stor del som er farget rød i figurene med 3 farger, 4 farger og 5 farger.
Kan du finne en generell sammenheng?
Kan du bevise at denne sammenhengen alltid gjelder?
Ekstra
Hva med delene som er farget oransje, gule osv.?
Kan du finne en generell sammenheng her?
Kan du bevise at dette er riktig?
Starthjelp
Tenk deg at radien i den minste halvsirkelen er x.
- Hva er da radiene i alle de andre halvsirklene?
- Hvilke arealer kan du regne ut ved hjelp av x og π?
Løsning
Denne oppgaven kan løses på veldig mange måter. Men alle tar utgangspunkt i at figuren kan deles i mange halvsirkler ved at vi tegner inn en diameter i sirkelen.
På figuren står bokstavene A, B og C for henholdsvis det røde, det oransje og det gule arealet som ligger på oversiden av diameteren.
Vi kaller radien i A for x. Arealet av A er \(A=\frac12 \pi x^2\).
Radien i halvsirkelen B er \(2x\), og arealet av B er arealet av halvsirkelen med radius \(2x\) minus areal A: \(B=\frac12 \pi (2x)^2 - \frac12 \pi x^2=\frac32 \pi x^2\).
Radien i halvsirkelen C er \(3x\), og arealet C er en halvsirkel med radius \(3x\) minus en halvsirkel med radius \(2x\):
\(C=\frac12 \pi (3x)^2-\frac12 \pi (2x)^2=\frac52 \pi x^2\).
Vi bruker symmetri for å regne ut de fargede arealene:
Rødt areal = \(A+C=3 \pi x^2\)
Oransje areal = \(2B= 3 \pi x^2\)
Gult areal = \(A+C=3 \pi x^2\)
Vi ser at de tre arealene er like store, for alle er \(\frac{1}{3}\) av sirkelens areal.
Når vi skal generalisere, kan vi kalle arealene på oversiden av diameteren i den store sirkelen for A1, A2, …, An. Og vi lar den store sirkelen ha radius r.
Da er A1 en halvsirkel med radius \(\frac rn\), og hvert areal \(A_k\) er en halvsirkel med radius \(\frac{kr}n\) minus en halvsirkel med radius \(\frac{(k-1)r}n\).
\(A _{k}=\frac{\pi}{2} \left(\frac{k^2r^2}{n^2} -\frac{(k-1)^2r^2}{n^2}\right)=\frac {\pi r^2}{2n^2}(2k-1)\).
Hvert areal med farge nummer k består av arealet \(A_k\) pluss arealet \(A_{n+1-k}\). Det blir slik fordi arealene på undersiden av diameteren er delt opp på samme måte som på oversiden.
Samlet areal med farge k blir da
\(A_k+A_{n+1-k} \\ = \frac {\pi r^2}{2n^2}(2k-1)+\frac {\pi r^2}{2n^2}(2(n+1-k)-1)\\ =\frac {\pi r^2}{2n^2}(2k-1+2n+2-2k-1)\\ =\frac {\pi r^2}{n}\)
Dette er \(\frac1n\) av det totale arealet \(\pi r^2\), og alle fargene vil dekke en like stor del av sirkelen.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Denne oppgaven gir elevene anledning til å øve på å beregne arealer av halvsirkler og arbeide med π. De får et overraskende resultat som inviterer til generalisering.
Mulig tilnærming
Oppgaveark som kan skrives ut, finner du her.
En PowerPoint-fil med en figur på hvert ark finner du her.
Det er en fordel om elevene har passere tilgjengelig – det gjør tegningen lettere og finere.
Begynn med å vise bildene i PowerPoint-fila, men ikke for lenge. Så får ikke elevene se på bildene lenger.
«Tenk på bildene dere nettopp så. Prøv å tegne det du så. Kan du forklare sidemannen/arbeidspartneren din hvordan tegningene var laget?»
Vis fram bildene på nytt, slik at elevene kan sammenligne dem med det de har tegnet. Å tegne det de har sett, gir god øvelse i å tegne med passer.
«Nå når dere har sett hvordan tegningene er laget, kan dere snakke sammen to og to og prøve å finne ut hvordan dere skal regne ut arealene av figurene i de ulike fargene.» Gi elevene tid til å diskutere før du igjen samler klassen for å dele forslagene til løsningsmetoder. Så kan du be alle om å bruke disse metodene til å regne ut arealet av hvert enkelt område.
Elevene kan trenge hjelp til å komme på å velge en bokstav som kan representere radien i den minste halvsirkelen. Kanskje vil noen heller velge en enhetslengde i stedet for en bokstav. Det går fint an, men elevene må forstå at det er fordi vi her regner ut deler av en helhet.
Overraskende nok har alle de fargede områdene like stort areal. Så snart elevene har regnet ut arealene i figuren med tre farger, kan de arbeide videre med figurene med fire og fem farger.
Å bevise det generelle tilfellet, at alle områdene vil få like stort areal, er ganske utfordrende. Men det kan gjøres litt enklere ved å bare først vise at det første arealet (det som ligger slik som de røde arealene på figurene) alltid utgjør 1/n av sirkelens areal når den er delt opp i n bøyde arealer.
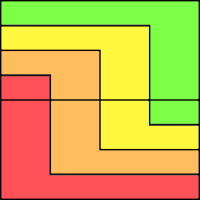
Figuren nedenfor har et tilsvarende mønster med rektangler. Det kan brukes for å generalisere uten å måtte regne med π.
Gode veiledningsspørsmål
- Hvor er sentrum i alle halvsirklene i figuren?
- Hva er sammenhengen mellom de ulike radiene?
- Hvordan kan du regne ut arealene for en sirkel med n ulike fargede områder?
Mulig utvidelse
Vis algebraisk at alle områdene har like stort areal for en sirkel som er delt opp i n fargede områder (se under Løsning).
Ressursen er utviklet av NRICH