Kirkevindu

Stikkord: Omkrets Sirkler

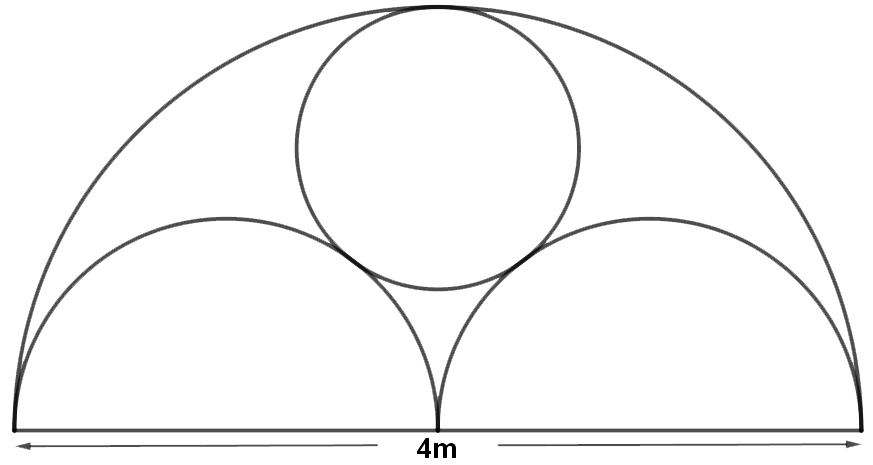
Den øverste delen av et kirkevindu har form som en halvsirkel. Inne i halvsirkelen er det to mindre halvsirkler og en sirkel, som tangerer hverandre slik figuren viser. Bredden på vinduet er 4 m.

Hvor stor er radien i sirkelen i meter?

En halvsirkel med to halvsirkel og en sirkel i

Marker sentrum i sirkelen og i de to små halvsirklene.
Trekk noen hjelpelinjer mellom punktene. Hvor lange er disse linjestykkene?
Hva er avstanden fra sentrum i sirkelen til sentrum i den store halvsirkelen?
Kan du finne en trekant i figuren som kan hjelpe deg med utregningen?

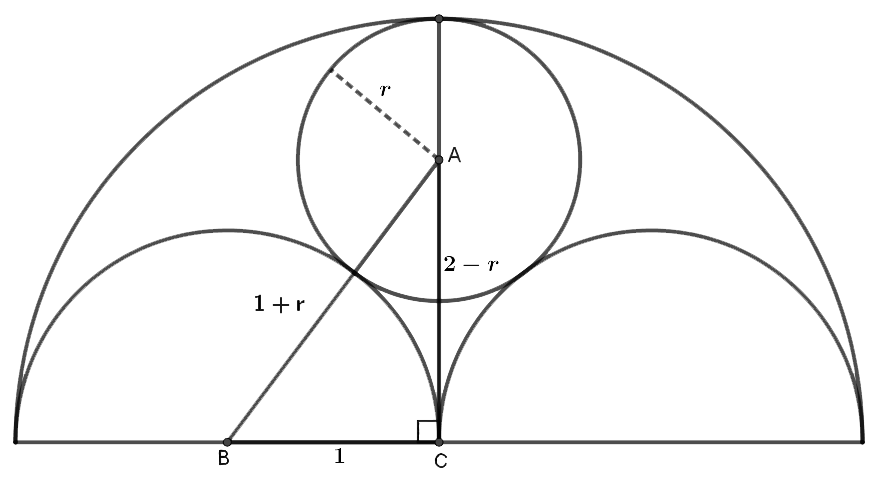
La A være sentrum i sirkelen, og la sirkelens radius være r. C er sentrum i den store halvsirkelen, og B er sentrum i en av de små halvsirklene.

En halvsirkel med to halvsirkel og en sirkel i, og noen linjer

Da er BC = 1 m, siden den er en firedel av vinduets bredde.

AC = (2 - r) m = den store halvsirkelens radius – sirkelens radius

BA = (1 + r) m = radius i den lille halvsirkelen + sirkelens radius

Trekanten ABC er rettvinklet, vinkel C = 90^o.

Vi bruker Pytagoras’ setning:

$\begin{align} (1+r)^2&=1^2+(2-r)^2\\ 1+2r+r^2&=1+4-4r+r^2\\ 6r&=4\\ r&=\frac23\\ \end{align}$

Sirkelens radius er $\frac23 \:m$ .

Ressursen er utviklet av NRICH

Kirkevindu

Problem

Starthjelp

Løsning