En uvanlig polygon
Problem
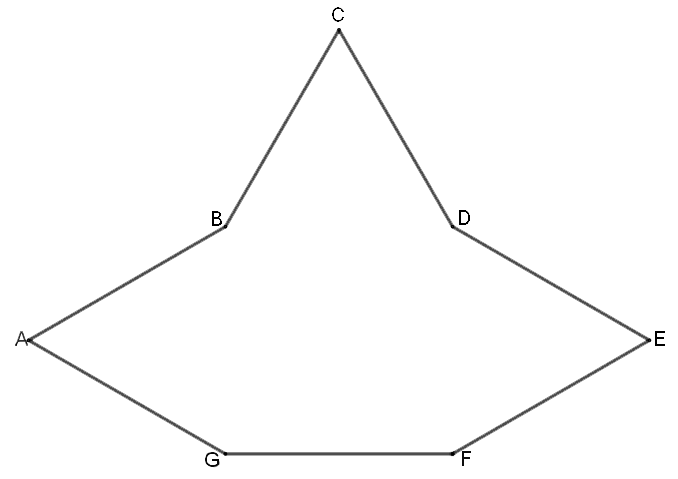
Figuren viser en polygon (mangekant) ABCDEFG der FG = 6, og
GA = AB = BC = CD = DE = EF.
BDFG er et kvadrat.
Arealet av hele polygonen er nøyaktig dobbelt så stort som arealet av BDFG.
Finn omkretsen av hele polygonen.
Løsning
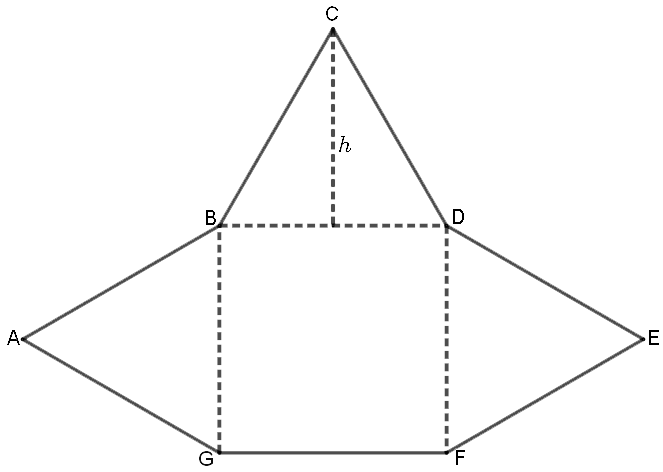
Arealet av kvadratet BDFG er \(6 \cdot 6 = 36\) kvadratenheter.
Da er også arealet av de tre trekantene ABG, BCD og DEF til sammen \(36\) kvadratenheter, og arealet av hver av trekantene er \(12\) kvadratenheter.
Trekantene er kongruente, og vi velger å finne BC ved hjelp av arealet av trekanten BCD.
\(\frac12\cdot6\cdot h = 12\\\)
\(h = \frac{12}{3} = 4\)
\(BC^2=(\frac{BD}2)^2+4^2\\\)
\(BC^2=3^2+4^2\\\)
\(BC^2=25\\\)
\(BC=5\)
Omkretsen er \(6 \cdot5 + 6 = 36\) enheter
Ressursen er utviklet av NRICH
10