Ny duk hver dag
Aktivitet
Karl har laget en serie duker, en for hver dag! Han vil bruke flest mulig farger i hver duk, men han stiller forskjellige krav til symmetrier i dukene.
Han lar mønsteret i alle dukene være ruter, og duker med 5 · 5 ruter passer på bordet hans.
Mandag
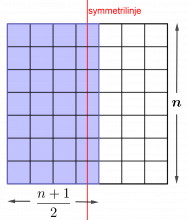
På mandag skal duken ha bare én symmetrilinje.
Design duker i andre størrelser som har bare én symmetrilinje.
Kan du finne en måte å beregne største antall farger som trengs til en n · n -duk med bare én symmetrilinje? (La n være et oddetall, og la mønsteret bestå av ruter slik som på Karls duk.)
Tirsdag
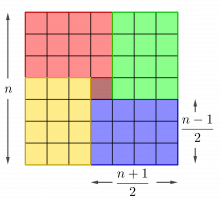
På tirsdag skal duken ha rotasjonssymmetri av orden 4* og ingen symmetrilinjer.
*Rotasjonssymmetri av orden 4 betyr at hvis figuren roteres om et fast punkt, figurens sentrum, gjennom et helt omløp (360˚), vil den være lik den opprinnelige figuren fire ganger, dvs. for hver rotasjon på 90˚.
Design duker i andre størrelser som har rotasjonssymmetri av orden 4 og ingen symmetrilinjer.
Kan du finne en måte å beregne største antall farger som trengs til en n · n -duk med rotasjonssymmetri 4 og ingen symmetrilinje? (La n være et oddetall, og la mønsteret bestå av ruter slik som på Karls duk.)
Onsdag
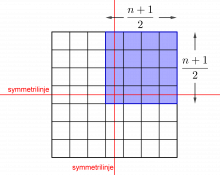
På onsdag skal duken ha to symmetrilinjer (horisontalt og vertikalt) og rotasjonssymmetri av orden 2.
Design duker i andre størrelser som har to symmetrilinjer (horisontalt og vertikalt) og rotasjonssymmetri av orden 2.
Kan du finne en måte å beregne største antall farger som trengs til en n · n -duk med 2 symmetrilinjer (horisontalt og vertikalt) og rotasjonssymmetri av orden 2? (La n være et oddetall, og la mønsteret bestå av ruter slik som på Karls duk.)
Torsdag
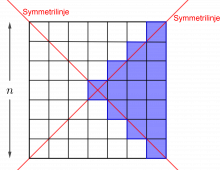
På torsdag skal duken ha to symmetrilinjer (diagonale) og rotasjonssymmetri av orden 2.
Design duker i andre størrelser som har to symmetrilinjer (diagonale) og rotasjonssymmetri av orden 2.
Kan du finne en måte å beregne største antall farger som trengs til en n · n -duk med to symmetrilinjer (diagonale) og rotasjonssymmetri av orden 2? (La n være et oddetall, og la mønsteret bestå av ruter slik som på Karls duk.)
Fredag
På fredag skal duken ha fire symmetrilinjer og rotasjonssymmetri av orden 4. (En figur med rotasjonssymmetri av orden 4 vil gjenta seg selv fire ganger i løpet av en rotasjon på 360˚.)
Design duker i andre størrelser som har fire symmetrilinjer og rotasjonssymmetri av orden 4.
Kan du finne en måte å beregne største antall farger som trengs til en n · n -duk med fire symmetrilinjer og rotasjonssymmetri av orden 4? (La n være et oddetall, og la mønsteret bestå av ruter slik som på Karls duk.)
Ekstra: Lørdag og søndag
I helgene vil Karl ha duker der antall ruter er partall.
Undersøk hvor mange farger som trengs for de forskjellige typene av symmetrier i duker med n · n ruter når n er et partall.
Starthjelp
- Hvor mange ekstra farger må du ha for å gå fra et 5 · 5 -mønster til et 7 · 7 -mønster?
- Hvor skal de ekstra fargene plasseres?
- Hvor mange ekstra farger må du ha for å gå fra et 7 · 7-mønster til et 9 · 9-mønster?
- Hvor skal de ekstra fargene plasseres?
- Hvor mange ekstra farger trengs i et 11 · 11-design?
- Hvor skal de ekstra fargene plasseres?
Løsning
Mandag
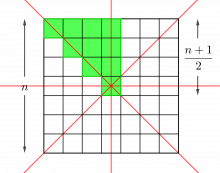
I 5 · 5 -duken kan det høyst være 15 ulike farger.
Fargene i kolonnene til venstre for den midterste (kolonnen med symmetrilinje) blir speilet i kolonnene til høyre for den midterste. Så hvis vi har et n · n -kvadrat der n er et oddetall, er det maksimale antall farger som kan brukes `n · (n+1)/(2)`.
Tirsdag
I \(5\cdot5\)-duken kan det høyst være 7 ulike farger.
Når vi har rotasjonssymmetri av orden 4, må de fire rektanglene (som er markert med ulike farger) være like. I tillegg kommer ruta i midten. Så det største antall farger som kan brukes i et \(n\cdot n\) kvadrat, er
\(\frac{n+1}{2} \cdot \frac{n-1}{2}+1=\frac{n^2-1}{4}+1=\frac{n^2+3}{4}\).
Onsdag
I \(5\cdot5\)-duken kan det høyst være 9 ulike farger.
Hvis vi har ulike farger i alle rutene i det blå kvadratet, kan vi speile fargene om begge de markerte symmetrilinjene. Det blir dessuten rotasjonssymmetri av orden 2, for hvis vi roterer figuren om sentrum 180˚, får vi en figur som er lik den vi begynte med. Største antall farger vi kan bruke her, er \((\frac{n+1}{2} )^2\).
Torsdag
I \(5\cdot5\)-duken kan det høyst være 9 ulike farger.
Hvis vi lar alle rutene i det fargede området ha ulike farger, kan vi lage symmetri om diagonalene. Vi vil også få rotasjonssymmetri av orden 2. Det største antall farger vi kan bruke på denne n x n-duken, er
1 + 3 + 5 + … + n, der n er et oddetall.
Husk: Summen av de k første påfølgende oddetallene er \(1+3+5+ ...+(2k-1)=\frac{(1+2k-1)\cdot k}{2}=k^2\).
Da er summen \(1+3+5+... + n=(\frac{n+1}{2})^2\), der n er et oddetall.
Fredag
I \(5\cdot5\)-duken kan det høyst være 6 ulike farger.
Hvis vi lar alle rutene i det fargelagte området få ulike farger, kan vi fortsette fargeleggingen slik at det blir symmetrilinjer både horisontalt, vertikalt og diagonalt, som på figuren. Da får vi også rotasjonssymmetri av orden 4.
Største antall farger vi kan bruke, er \(1+2+...+\frac{n+1}{2}= \frac{(1+\frac{n+1}{2} )\cdot \frac{n+1}{2}}{2}=\frac{(n+3)(n+1)}{8}\).
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Vi lar ofte elevene finne mønstre ved å registrere hvordan en serie figurer utvikler seg. Dette problemet utfordrer dem til å generalisere ved å studere strukturene i ulike symmetriske mønstre, og de må forklare hvordan de finner generelle regler eller formler.
Mulig tilnærming
Disse kopieringsoriginalene kan være nyttige:
Oppgaven
Ark med rutenett til å fargelegge
PowerPoint som viser dukene for hver dag
De fem dukene er illustrert på hver sin kopieringsoriginal:
Mandag
Tirsdag
Onsdag
Torsdag
Fredag
«Disse dukene er symmetriske. Kan dere beskrive hvilke typer symmetrier de har?»
Så snart elevene har oversikt over hvilke symmetrier som gjelder for hver av dukene:
«For hver av symmetrireglene ønsker jeg at dere skal finne det maksimale antall farger dere kan bruke i duker med størrelse \(5\cdot5\), \(7\cdot7\) og \(9\cdot9\). Alle dukene skal ha rutemønster, slik som dukene på figurene.»
«Om en stund vil jeg be dere finne maksimalt antall farger i mye større duker, duker som er for store til å tegne. Så dere må notere det dere finner ut om de mindre dukene, og tenke over hvordan dette kan hjelpe dere til å finne regler og formler som kan gjelde for alle slike duker, uansett hvor store de er.»
Her kan du gi elevene kopier av arkene der de selv kan fargelegge. Det kan være en god hjelp for å tenke ut hva en må ta hensyn til, og hvilke regler som må følges. Etter hvert som de blir ferdige, kan arkene henges opp slik at elevene kan se hverandres løsninger. Du må henge dem opp slik at de som følger samme regel, henger samlet.
«Tenk dere at jeg ville ha en duk med \(99\cdot99\) ruter. Hvor mange farger ville jeg da trenge for hver av symmetriene? Dere må komme fram til overbevisende argumenter som forklarer hvordan dette problemet skal løses. Kanskje kan dere også komme fram til hvordan vi skal finne maksimalt antall farger for hver av symmetriene i en duk med \(n\cdot n\) ruter.»
La elevene arbeide i par med denne utfordringen. La så parene gå sammen, slik at de i grupper på fire kan bearbeide og forfine argumentene for ett eller to design. Til slutt kan du be noen av disse gruppene om å presentere sine overbevisende argumenter for resten av klassen, som må ha rollen som kritiske venner og foreslå forbedringer i argumentene.
Mulig utvidelse
Be elevene finne ut hvor mange farger som trengs til hver regel i duker med størrelse n x n når n er et partall.
En svært utfordrende utvidelse av oppgaven er å finne en kombinert regel som gjelder både når n er oddetall og partall – for hver av symmetritypene.
Mulig støtte
Stålkabler, er en annen god øvelse der elevene må finne algebraiske regler ut fra geometriske mønstre.
Ressursen er utviklet av NRICH