Fire kvadrater
Problem
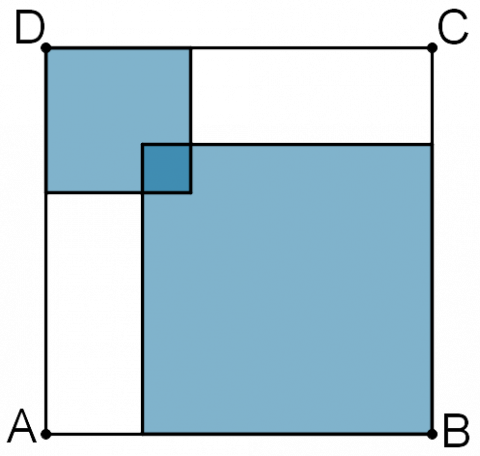
Kvadratet ABCD har areal 196. Det inneholder to overlappende kvadrater. Det største av dem har et areal som er fire ganger så stort som arealet av det minste. Arealet av området der de overlapper hverandre, er 1.
Hvor stort er det fargede arealet på figuren?
Løsning
Det store kvadratet har areal 196 = 142, så sidene har lengde 14.
Siden forholdet mellom det store fargede kvadratet og det lille fargede kvadratet er 4 : 1, er forholdet mellom sidelengdene i de to kvadratene 2 : 1.
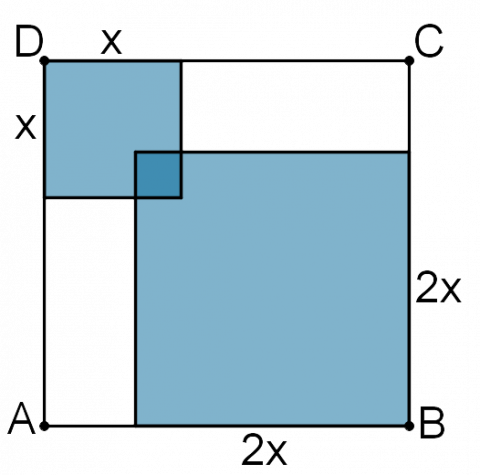
Hvis vi setter sidelengden i det lille fargede kvadratet lik x, har det store fargede kvadratet sidelengde 2x.
Figuren er symmetrisk om diagonalen BD, så området der de to kvadratene overlapper hverandre, er også et kvadrat. Siden dette har areal 1, har det også sidelengde 1.
Da må x + 2x - 1 = 14, og altså x = 5.
Areal av det lille fargede kvadratet er 52 = 25.
Areal av det store fargede kvadratet er 102 = 100.
Samlet farget areal er 25 + 100 – 1 = 124.
Ressursen er utviklet av NRICH