Utenfor nikanten
Problem
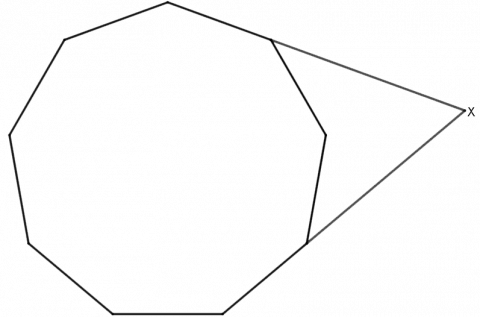
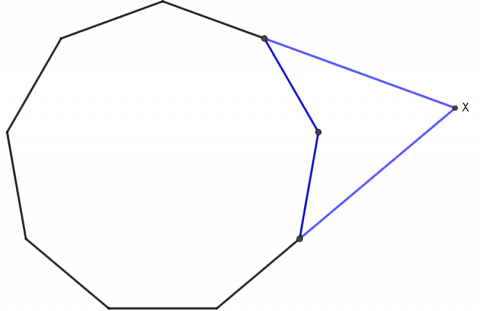
I en regulær mangekant er alle sidene like lange og alle vinklene like store. Figuren viser en regulær mangekant med ni sider, en nikant (eller en nonagon). To av sidene er forlenget slik at de møtes i punktet X.
Hvor stor er den spisse vinkelen i X?
Starthjelp
Her er noen metoder som du kan bruke for å finne vinklene i regulære nikanter:
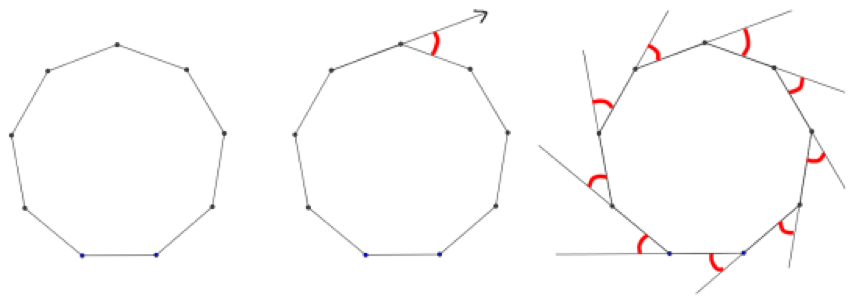
Se for deg at du går rundt en regulær nikantet park.
Det andre bildet viser vinkelen du må svinge når du kommer til det første hjørnet.
Det tredje bildet viser alle vinklene du må svinge for å komme rundt hele parken én gang.
– Hvor mange grader svinger du til sammen?
– Hvor stor må hver vinkel på utsiden være?
– Hvor stor må hver vinkel på innsiden være?
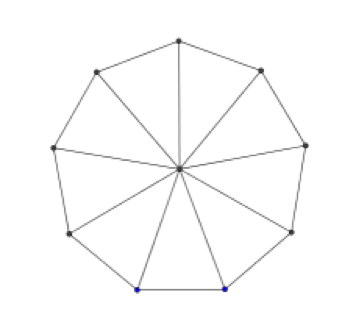
Her ser du en regulær nikant.
Den har blitt delt opp i ni likebeinte trekanter.
Hva er summen av alle vinklene i alle trekantene?
Subtraher vinklene som dannes rundt sentrum, slik at du finner summen av alle vinklene i hjørnene til nikanten.
Hvor stor må hver vinkel i nikanten være?
Løsning
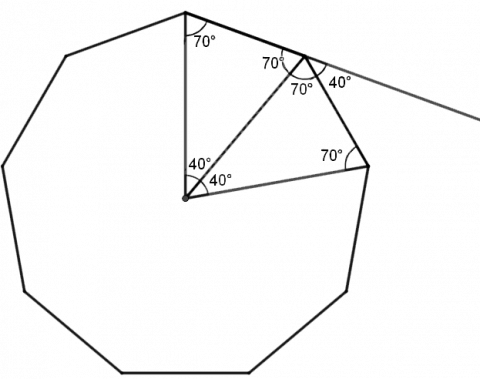
Figuren viser at vi kan dele nikanten inn i ni kongruente, likebeinte trekanter. Hver trekant vil ha en vinkel på 360° : 9° = 40° og to vinkler på 70°. Da er vinklene i hvert hjørne i nikanten på 140°, og de ytre vinklene til en regulær nikant er på 40°.
Vi kjenner tre av vinklene i den blå firkanten, to vinkler er på 40° og en er på 360° - 140° = 220°, til sammen blir det 300°. Vinkelsummen i en firkant er 360°, så den spisse vinkelen ved X er på 60°.
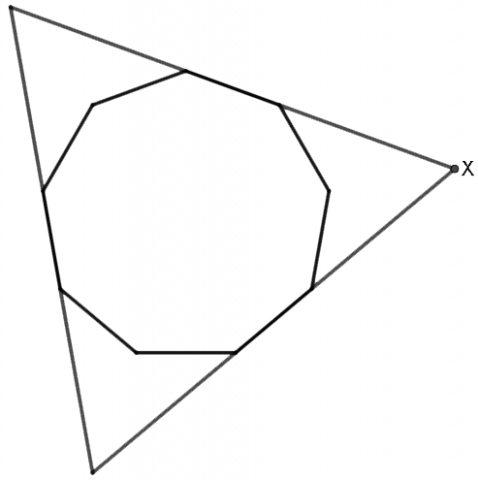
Vi kan også se at den regulære nikanten passer nøyaktig inn i en likesidet trekant:
Ressursen er utviklet av NRICH