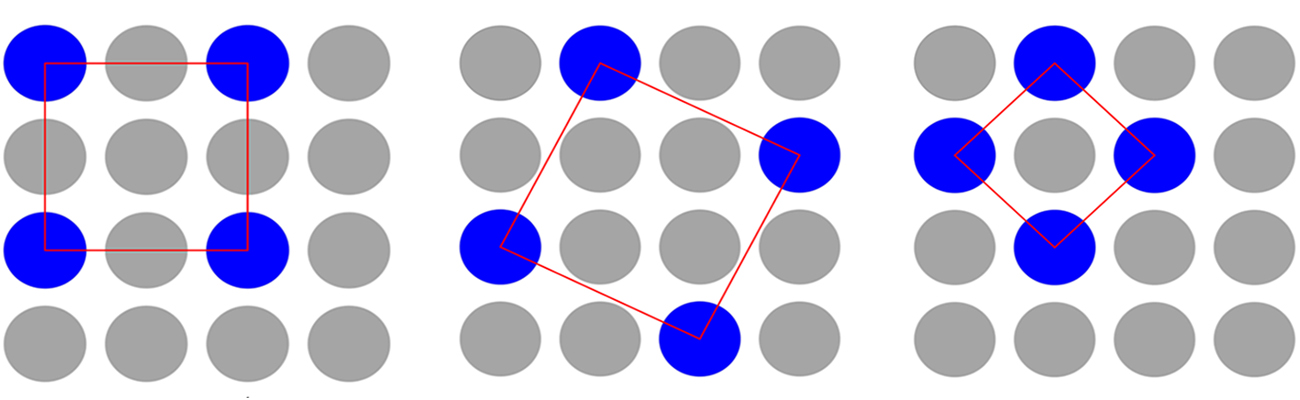
Kvadrathjørner

Hvorfor arbeide med denne oppgaven?

Dette problemet utfordrer elevenes forståelse av kvadratbegrepet, da kvadrater ikke trenger å være orientert slik at sidekantene går horisontalt og vertikalt. Det er også en god kontekst som legger opp til systematiske tilnærminger til problemløsning.

Mulig tilnærming

Du kan begynne med å spille spillet «Lag kvadrater» noen ganger sammen som klasse. Det legger til rette for en diskusjon om hva som gjør et kvadrat til et kvadrat, og du kan få fram misoppfatninger om at kvadrater «på skrå» ikke er kvadrater, men for eksempel «diamanter».

Introduser problemet ved å bruke det store rutenettet på en interaktiv tavle, eller bruk det interaktive verktøyet, og be elevene arbeide med problemet sammen i par. De kan bruke det store rutenettet og tellebrikker, eller denne kopioriginalen med mindre rutenett. Minn elevene på at det er om å gjøre å legge på så mange tellebrikker som mulig, uten å lage kvadrater! Etter en stund kan elevene dele resultatene sine så langt. Hva er det største antall tellebrikker hittil? Be et par elever om å gjenskape løsningsforslaget sitt på storskjermen, slik at de andre kan kontrollere at de ikke har noen kvadrater.

Deretter kan du utfordre klassen til å finne en strategi som vil sikre at det største antallet mulige tellebrikker blir funnet. Hvordan kan de vite at alle mulige kombinasjoner er testet? Noen elever kan for eksempel foreslå et system som er basert på å plassere tellebrikker fra øverst til venstre til nederst til høyre hver gang, og sjekke at de ikke får et kvadrat for hvert nytt «lag» de legger på. Du kan også modellere begynnelsen på en strategi, og gi elevene tid til å utforske problemet.

I plenum kan dere diskutere løsninger og hva som gjør én løsning forskjellig fra en annen. Vil dere vurdere rotasjoner og speilinger av brikkenes plassering på brett som like eller som forskjellige løsninger?

Gode veiledningsspørsmål

• Hvordan kan du være sikker på at du har funnet det største antallet tellebrikker du kan legge på?
• Er du sikker på at det ikke er noen kvadrater i rutenettet ditt?

Mulig utvidelse

Elevene kan undersøke større rutenett og se om de finner et mønster i hvor mange tellebrikker de kan legge på. Da kan det også være lurt å undersøke mindre rutenett. Er det mulig å forutsi hvor mange tellebrikker det er plass til på et hvilket som helst rutenett?

Du kan bruke dette interaktive verktøyet for å sjekke løsninger for større rutenett.

Mulig støtte

Noen elever kan begynne med et 3 x 3-rutenett.