Kompistal
Aktivitet
Sjå på denne talrekkja:
10 15 21 4 5
Talrekkja er slik at viss du adderer to tal som står ved sida av kvarandre, blir summen eit kvadrattal:
10 + 15 = 25
15 + 21 = 36
21 + 4 = 25
4 + 5 = 9
Kan du lage ei talrekkje med alle tala frå 1–17, slik at summen av to tal som står ved sida av kvarandre, blir eit kvadrattal?
Du kan skrive ut tala ved å laste ned kopioriginalen i menyen til venstre. Dei kan vere til hjelp for å teste ut ulike talrekkjer.
Kan du lage fleire ulike talrekkjer med dei same tala? Viss ikkje, kan du vere heilt sikker på at løysinga di er unik?
Starthjelp
Er det nokre tal som kan adderast med berre eitt tal for at summen skal bli eit kvadrattal?
Kor skal desse tala i så fall plasserast?
Løysing
Éin måte å løyse denne oppgåva på er å setje opp alle kvadrattala til og med 33, sidan 16 + 17 = 33 er det største talet vi kan få.
1 – 4 – 9 – 16 – 25
Det betyr at for 17 og 16 er det berre éi moglegheit nemleg 25, så dei må stå i kvar sin ende. 16 blir addert med 9 og blir sette i den eine enden. 17 må adderast med 8, og 8 må adderast med 1 sidan det er berre eitt 8-tal. Etter 1 er det to moglegheiter, både 3 og 15 vil fungere, men ettersom 15 berre går an med 1 og 10, må 15 setjast her, og så 10. Deretter er det berre éi løysing for kvart nytt tal til vi til slutt har denne rekkja:
16 – 9 – 7 – 2 – 14 – 11 – 5 – 4 – 12 – 13 – 3 – 6 – 10 – 15 – 1 – 8 – 17
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
I denne aktiviteten må elevane tenkje strategisk og utarbeide overbevisande argument og grunngi funna sine. For å kunne gjere denne aktiviteten bør elevane likevel ha kunnskapar om kvadrattal.
Mogleg tilnærming
Introduser problemet ved å bruke dømet 10, 15, 21, 4, 5, og forklar at denne talrekkja er spesiell, fordi kvart par addert gir eit kvadrattal. Så skal elevane parvis eller i grupper på tre laga ei liknande talrekkje ved å bruke tala frå 1 til 17. Del gjerne ut tala frå kopioriginalen som dei kan bruke som konkretar.
Når para eller gruppene byrjar å finne dei første løysingane, kan du informere elevane om at du ønskjer å vite alle moglege måtar å lage ei slik talrekkje på. Utfordre dei til å utarbeide overbevisande argument som forklarer at dei har funne alle moglege måtar.
På slutten av aktiviteten bør elevane få høve til å vise framgangsmåtane og løysingane sine til kvarandre.
Ein alternativ måte å byrje aktiviteten på er å spørje 17 frivillige om å stille seg opp på ei rekkje og halde eit tal kvar. Deretter skal resten av klassen plassere dei slik at talrekkja følgjer kriteria som gitt i oppgåva. Når elevane har funne ei løysing, kan dei arbeide i par for å prøve å finne nye løysingar og utarbeide argument for at dei har funne alle.
Gode rettleiingsspørsmål
- Er det nokre tal som ikkje kan stå saman?
- Er det nokre tal som berre kan stå saman med eitt tal?
- Er det nokre tal som berre kan stå saman med to tal?
- Er det nokre tal som kan stå saman med fleire enn to tal?
- Korleis kan du vere sikker på at du har funne alle moglege løysingar?
Mogleg utviding
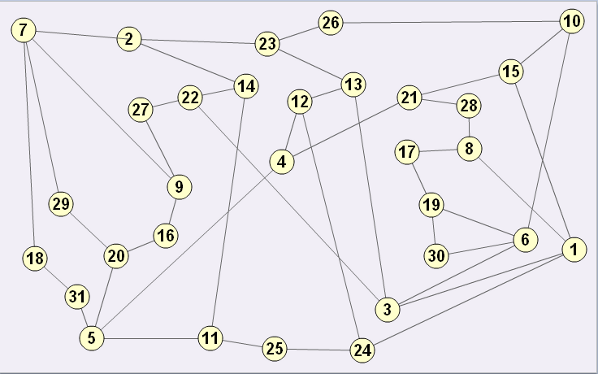
Grafen under har punkt med nummer frå 1 til 31. Kvar linje knyter saman to tall, og viss du adderer dei to tala, får du eit kvadrattal.
Bruk grafen til å lage ei tallinje med tala 1–31 slik at tala som står saman to og to, gir et kvadrattal til sum. Finst det meir enn éi løysing?
Kan du finne kva som helst anna tal n mindre enn 31 som gjer at alle tala frå 1 til n kan danne ei tallinje på same måte? Korleis kan grafen vere til hjelp?
Mogleg støtte
Foreslå for elevane at dei kan lage ein tabell der dei kan notere tala som addert gir eit kvadrattal.
Illustrasjonsfoto: Kyle Hinkon on Unsplash
Ressursen er utviklet av NRICH