Prismeutfordring
Aktivitet
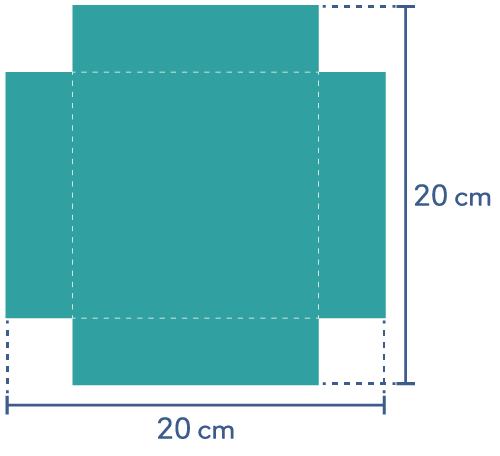
Klipp ut like kvadrat i alle fire hjørna i eit ark på 20 cm x 20 cm. Brett opp sidene slik at du får ei eske utan lokk.
Kva er volumet av eska di?
Kva for forskjellige volum kan du lage ved å variere storleiken på kvadrata du klipper ut?
Kor stort kan volumet maksimalt bli i ei slik eske som du lagar av eit ark på 20 cm x 20 cm?
Når du har svart på spørsmåla ovanfor, kan du ta utgangspunkt i kvadratiske ark som ikkje har sidelengde 20 cm.
Kan du finne eit forhold mellom storleiken på papiret og storleiken på kvadrata du klipper ut, som gir størst mogleg volum?
Starthjelp
Her er det lurt å arbeide systematisk.
Begynn med å klippe vekk kvadrat med sidelengde 1 cm i kvart hjørne. Kva blir volumet då?
Deretter klipper du vekk 2 cm, 3 cm osv.
Sidelengda i kvadrata du klipper vekk, treng ikkje nødvendigvis å vere heile tal.
Kanskje du kan bruke eit rekneark til å hjelpe deg med utrekningane dine?
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
Dette er eit godt eksempel på ei oppgåve med låg inngangsterskel og stor takhøgde, som kan løysast på forskjellige måtar. Oppgåva legg til rette for visualisering, 2D-representasjon av 3D-former og volumrekning, og elevane kan introduserast for tanken om å finne den optimale løysinga – eit viktig poeng i matematikk. Sidan det er mange måtar å gå laus på utfordringa, kan dei erfare nye måtar å resonnere matematisk på, gjennom numeriske, algebraiske og grafiske representasjonar. Somme kan også finne ein samanheng som kan uttrykkjast som ein funksjon.
Mogleg tilnærming
Del ut kopioriginalen som inneheld oppgåveteksten.
«Tenk deg at du har eit kvadratisk ark på 20 cm x 20 cm. Sjå for deg at du klipper vekk kvadrat med sidelengde 5 cm i kvart hjørne, og bretter opp sidene slik at du får ei eske utan lokk. Kva blir måla på denne eska? Diskuter med ein medelev. Kva blir volumet av eska?»
La elevane snakke litt saman før de diskuterer i plenum og blir einige om måla på og volumet av ei slik eske. Elevane skal forklare korleis dei fann måla og volumet. Det kan vere lurt å bruke ein tabell eller å teikne opp den ferdige eska på tavla.
«Kan vi kan lage ei eske med større volum?»
La elevane få litt tid til å arbeide saman i par for å utforske korleis kvadrat med forskjellige storleikar påverkar volumet av eska. Deretter kan du samle inn resultat i ein tabell eller eit rekneark.
«Kva er det største volumet vi har funne til no? Kan vi finne noko endå større?»
Be elevane om å sjå etter og kommentere mønster dei ser i resultata, og foreslå metodar som kan føre til den optimale løysinga.
- Prøv og feil, med eller utan kalkulator.
- Bruk eit rekneark og ein formel som reknar ut volumet av ei eske med ein gitt storleik på kvadrata som skal klippast vekk.
- Finn ein formel eller funksjon, og bruk ein grafteiknar til å finne den maksimale verdien / den optimale løysinga.
Oppfordre nokre elevar til å prøve dei forskjellige metodane. Etter kvart samlar du klassen slik at de kan samanlikne og diskutere resultata.
Når elevane har funne den optimale løysinga for eit kvadrat på 20 cm x 20 cm, kan du gi forskjellige grupper kvart sitt utgangspunkt. Éi gruppe kan for eksempel begynne med eit kvadrat på 10 cm x 10 cm, ei anna med eit på 30 cm x 30 cm, osv. Kan elevane bruke ein av metodane for å finne den mest optimale løysinga for det nye kvadratet?
Til slutt samlar du informasjonen om dei utklipte kvadrata som gir størst volum for dei forskjellige utgangspunkta, og ber elevane om å sjå etter eit generelt mønster som vil fungere for kva som helst utgangspunkt.
Gode rettleiingsspørsmål
- Korleis kan du vere sikker på at du har funne det størst moglege volumet?
- Kan du overtyde nokre andre?
Mogleg utviding
I staden for å begynne med kvadratiske ark kan elevane undersøkje rektangulære utgangspunkt. For å gjere mønsterspottinga enklare kan det vere lurt å organisere dette, for eksempel ved å gi gruppene sett med rektangel der lengda er dobbel så lang som breidda, tre gonger så lang, fire gonger så lang, osv.
Elevane kan bruke algebra til å representere forholda dei finn, og dersom dei har kjennskap til funksjonar, kan dei bruke det til å finne det størst moglege volumet.
Mogleg støtte
Gi elevane ruteark på 20 cm x 20 cm, og la dei lage esker med forskjellige storleik. Oppfordre dei til å arbeide systematisk og halde orden på resultata sine.
Send inn elevsvar
Ressursen er utviklet av NRICH