Partal og oddetal
Aktivitet
Denne aktiviteten fungerer best når han blir gjennomført i samla klasse eller i ei stor gruppe, delt inn i fire mindre grupper. Kvar av gruppene får ein kopi av dei svarte korta, dei blå korta, dei raude korta eller dei grøne korta.
Kvar gruppe treng eit sett med kort i sin farge (same som fargen til gruppa). Kopioriginalar for svarte kort, blå kort, grøne kort og raude kort finn de i lista over kopioriginalar til venstre.
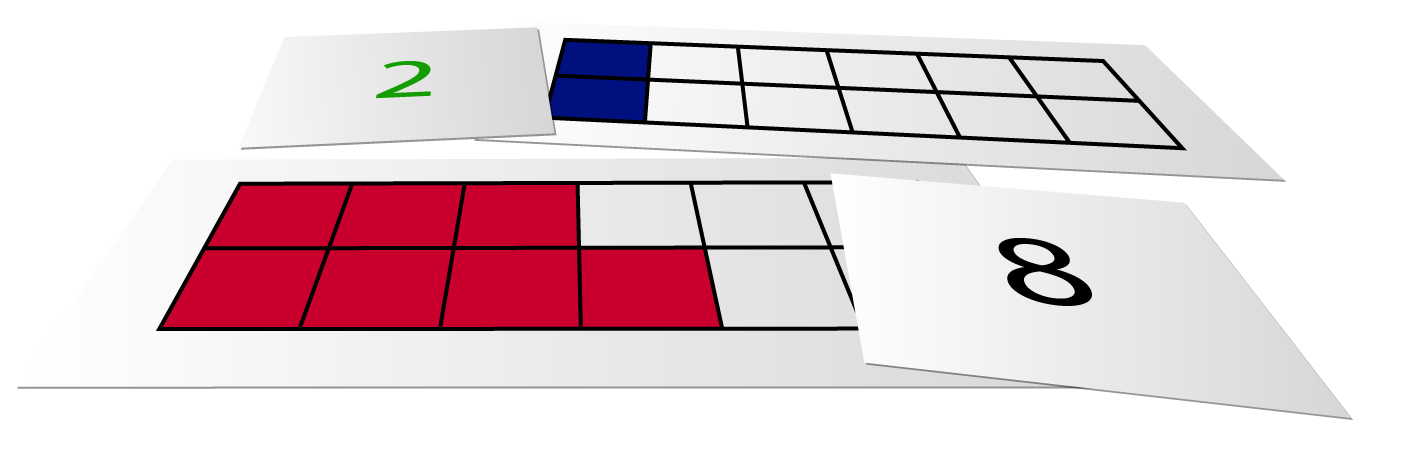
Gruppene legg korta sine slik at kvart talkort ligg ved sida av det kortet som har same antal farga kvadrat.
Bruk klossar som kan setjast saman, for eksempel multilink eller centikubar, og bygg tala på dei korta de har. Denne blokken viser 9:
9 er eit oddetal. Kan de sjå det ut frå forma på blokken? 8 er eit partal. Blokken for 8 er annleis enn blokken for 9. Kva er forskjellen?
Vel to av tala som de har bygt. Kva type tal får de når de adderer dei ved å setje saman dei to blokkane? Er det eit oddetal eller eit partal?
Vel to andre tal, og adder dei på same måten. Kva type tal får de denne gongen, partal eller oddetal?
Prøv dette på mange ulike måtar og med dei ulike blokkane dykkar. Kva ser de?
Korleis kan de notere funna dykkar?
Når får de eit oddetal?
Når får de eit partal?
Finn de eit mønster eller system? Kan de forklare kvifor det blir slik?
Starthjelp
Dersom de ikkje har multilink eller centikubar, kan de bruke bileta av dei fargelagde papirblokkane i kopieringsoriginalane. Klipp ut dei ulike blokkstorleikane, og vel blokkar som de set saman.
Løysing
Dette er ei artig oppgåve som handlar om partal og oddetal. Ho involverer både addisjon, teljing og generalisering. Ved å arbeide med denne aktiviteten kan elevane oppdage nokre generelle reglar som kan vere svært nyttige i andre oppgåver.
Mathias og Hanna har kome fram til denne løysinga:
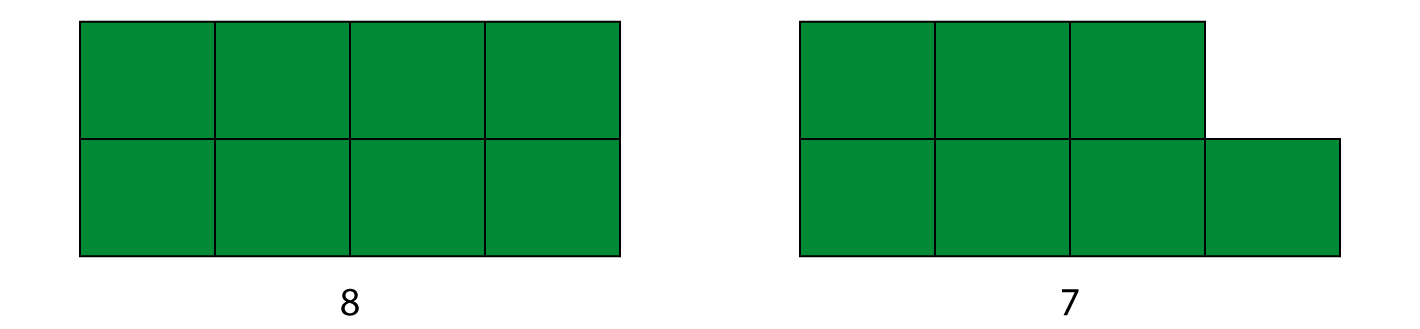
Partal har to like lange rader med klossar når vi byggjer dei, medan oddetal har ein ekstra kloss på den eine rada. Slik er alle tala, både partal og oddetal.
Når du adderer eit oddetal (med ein ekstra kloss) med eit partal (uten ein ekstra kloss), vil det nye talet bli eit oddetal (med ein ekstra kloss).
Når du adderer to partal (utan ekstra klossar), vil det nye talet bli eit partal (utan ekstra klossar).
Når du adderer to oddetal, vil det nye talet bli eit partal, fordi dei to ekstra klossane dannar eit nytt par.
O = oddetal, P = partal
O + O = P
P + P = P
P + O = O
Tre oddetal vil bli eit oddetal, for då blir det igjen ein ekstra kloss.
Fire oddetal vil bli eit partal, for då blir det to nye par med klossar frå dei fire ekstra klossane.
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
Aktiviteten er laga for arbeid i grupper, slik at elevane får sjå mange eksempel. Det gjer at dei kan konsolidere teljing og addisjon, og samtidig få erfaring med ulike representasjonar av partal og oddetal. Målet er at elevane skal kunne generalisere resultata av addisjon med partal og oddetal.
Mogleg tilnærming
La elevane samarbeide om å pare korta, slik at kvart tal ligg saman med det kortet som viser same antal farga kvadrat. Deretter gir du gruppene klossar (multilink, centikubar e.l.). Dei skal byggje modellar av kvart tal slik at modellane liknar på bileta av dei farga kvadrata. Det kan hende du må demonstrere dette, og då er det viktig at du set saman kubane slik at dei formar to rader, slik som med talet 9:
Samle klassen og be ei av gruppene om å velje to av talblokkane sine. Hald opp dei to blokkane, og spør elevane om nokon kan addere tala. Kor mange klossar blir det til saman? Be nokon vise det dei gjer, og forklare korleis dei tenkjer. Det kan kome ulike forslag til korleis ein kan setje saman dei to blokkane. Bruk tid på å utforske det. Kva for ein måte gjer det enklast å telje alle klossane? Lytt til forklaringane frå elevane, og trekk fram strategiar der dei tel toarar. Det er enklast dersom blokkane er sette saman av to rader med klossar. Her blir 9 og 11 adderte:
No skal gruppene undersøkje summen av ulike par av tal ved å bruke blokkane dei har laga. Elevane noterer ned det dei finn ut. Dei kan teikne, skrive, bruke klossane eller fargeleggje ruteark.
Etter at elevane har undersøkt summen av ulike talpar, samlar du dei igjen og seier at du har sett saman to blokkar akkurat slik dei har gjort. Den nye blokken du fekk, hadde 15 klossar. Spør elevane om dei kan finne ut kva for to tal (blokkar) du kunne sett saman. Medan dei kjem med forslag, teiknar du representasjonar av forslaga deira, for eksempel slik:
Teikn fleire eksempel på tavla, og spør elevane kva dei legg merke til. Kva er likt ved alle eksempla? Lytt til observasjonar frå elevane, og få tydeleg fram det som handlar om at nokre tal får blokkar som har ein ekstra kloss som stikk ut, medan andre tal får blokkar som er rektangulære – dei manglar ein kloss som stikk ut. Dersom elevane ikkje kjenner omgrepa partal og oddetal, introduserer du dei. Kva type tal er 15? La elevane setje ord på at når vi adderer eit oddetal og eit partal, får vi eit oddetal (eller at vi kan lage eit oddetal ved å addere eit partal og eit oddetal).
Gjer den same prosessen med eit partal, for eksempel 12. Kva for to tal kan vi addere og få 12? Teikn eksempel på tavla, og la elevane generalisere på same måten: Eit oddetal addert med eit oddetal gir eit partal, og eit partal addert med eit partal gir eit partal (eller at vi kan få eit partal ved å addere to oddetal, eller ved å addere to partal).
Gode rettleiingsspørsmål
- Korleis vil de setje saman korta/blokkane?
- Kan korta/blokkane setjast saman på forskjellige måtar?
- Kva tal har de alt prøvt?
- Fortel om det de har teikna og skrive. Kva ser de der?
- Ser de nokre system i det de har funne ut?
Mogleg utviding
Gjer ei liknande undersøking med subtraksjon. Kva finn de då?
Dersom de har berre einarar, trearar og femmarar (men kan bruke som mange de vil av kvar sort), kan de då lage 12 ved å bruke fire tal? Kan de finne ein måte å lage 13 på? Svarar elevane raskt nei på det siste spørsmålet, kan du gå ut frå at dei har forstått generalisering omkring addisjon av partal og oddetal.
Mogleg støtte
Dersom det er nok multilinkklossar eller centikubar, kan enkelte elevar byggje og bruke modellar av alle tala i staden for å teikne løysingar på papir.
Ressursen er utviklet av NRICH