Uoppstilte likningar
Aktivitet
Til denne aktiviteten treng du blå, grøne og raude brikker.
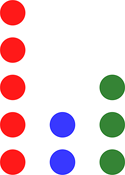
- Legg 10 brikker i tre kolonnar slik at
- den raude kolonnen inneheld 3 fleire brikker enn den blå kolonnen
- den grøne kolonnen inneheld 1 brikke meir enn den blå kolonnen
Kor mange brikker ligg det då i kvar av dei tre kolonnane?
La brikkene ligge slik til oppgåve 5.
- Løys oppgåve 1 ved hjelp av likningar.
Kor mange brikker er det i kvar kolonne?
- Bruk 10 brikker til å lage tre kolonnar slik at
- den blå kolonnen inneheld 3 færre brikker enn den raude kolonnen
- den grøne kolonnen inneheld 2 færre brikker enn den raude kolonnen
Kor mange brikker ligg det då i kvar av dei tre kolonnane?
La brikkene ligge slik til oppgåve 5.
- Løys oppgåve 3 ved hjelp av likningar.
Kor mange brikker er det i kvar kolonne?
- Samanlikn kolonnane frå oppgåve 1 og 3, og likningane frå oppgåve 2 og 4.
Forklar det du ser! Kvifor blir det slik?
- Bruk 13 brikker til å lage 3 kolonnar slik at
- den raude kolonnen inneheld 2 fleire brikker enn den blå kolonnen
- den grøne kolonnen inneheld 3 færre brikker enn den raude kolonnen
Kor mange brikker ligg det då i kvar av dei tre kolonnane?
- Løys oppgåve 6 ved hjelp av likningar.
Kor mange brikker er det i kvar kolonne?
- Bruk 12 brikker til å lage 3 kolonnar slik at
- den raude kolonnen inneheld 2 fleire brikker enn den blå kolonnen
- den grøne kolonnen inneheld 3 færre brikker enn den raude kolonnen
Kor mange brikker ligg det då i kvar av dei tre kolonnane?
- Lag minst to liknande oppgåver sjølv, og løys dei både ved hjelp av brikker og likningar.
- Ekstra utfordring
Bruk 20 brikker til å lage fire kolonnar slik at- den fjerde kolonnen inneheld like mange brikker som den andre og den tredje kolonnen til saman
- den første kolonnen inneheld 2½ gong så mange brikker som det er i den tredje kolonnen
Starthjelp
- Begynn med å lage tre kolonnar med raude, blå og grøne brikker.
- La forholdet mellom talet på brikker i kvar kolonne vere slik oppgåva seier. Kor mange brikker har du brukt no?
- Dersom du har brukt for mange brikker, kva må du gjere for å justere?
- Kva må du gjere dersom du har brukt for få brikker?
Når du skal løyse problema ved hjelp av likningar:
- Kor mange ukjende tal har du i ei likning?
- Kan du lage likningar med berre eitt ukjent tal?
- Kva tal vil du la vere ukjent?
Løysing
- Vi kan oversette til algebra på flere måter. Vi kan for eksempel si at
- vi har B blå brikker, R røde brikker og G grønne brikker
- da har vi R = B + 3 røde brikker og G = B + 1 grønne brikker
- vi har 10 brikker til sammen
Vi får likningenB + R + G = 10
B + (B + 3) + (B + 1) = 10
3B + 4 = 10
3B =6
B = 2
Det er 2 blå brikker, 2 + 3 = 5 røde brikker og 2 + 1 = 3 grønne brikker.
-
Det viser seg at vi får samme løsning som i oppgave 1. Men oversettelsen til algebra kan se annerledes ut.
-
Oversettelsen til algebra kan se annerledes ut:
-
vi har R røde brikker
-
det er B = R - 3 blå brikker og G = R - 2 grønne brikker
-
det er 10 brikker til sammen
R + B + G = 10R + (R – 3) + (R – 2) = 10
3R – 5 = 10
3R = 15
R = 5
Det er 5 røde brikker, 5 – 3 = 2 blå brikker og 5 – 2 = 3 grønne brikker.
-
-
Vi har satt opp to likninger som ser ulike ut, men som gir samme løsninger. Det er fordi vi kan velge hvilket tall som skal være det ukjente, i oppgave 1 var det antall blå brikker og i oppgave 3 var det antall røde brikker. Vi kunne også ha løst oppgaven med å la antall grønne brikker være den ukjente i likningen.
Når løsningen tolkes, dvs. oversettes til et svar på spørsmålet i oppgaven, blir løsningene de samme. -
Her kan vi for eksempel velge å ta utgangspunkt i antall røde brikker, R. Da er antall blå brikker B = R – 2 og antall grønne brikker er G = R – 3.
R + B + G = 13
R + (R – 2) + (R – 3) = 13
3R – 5 = 13
3R = 18
R = 6
Det er 6 røde brikker, 6 – 2 = 4 blå brikker og 6 – 3 = 3 grønne brikker.
-
Det er umulig å følge samme fordeling av brikker som i oppgave 6 og legge tre kolonner med brikker.
R + B + G = 12
R + (R – 2) + (R – 3) = 12
3R – 5 = 12
3R = 17
R = \(\frac{17}3\)
Likningen har en løsning, men det er ikke noe helt tall, og i disse oppgavene hvor vi skal kunne legge løsningene med brikker, er det bare hele tall som kan være løsninger. Konklusjonen er at likningen ikke har noen løsning.
Ekstra utfordring:
Vi velger å bruke fargene som på figuren, med lilla (L) i fjerde kolonne. Oversetter oppgaven til algebra.
- den fjerde kolonnen inneholder like mange brikker som den andre og den tredje kolonnen til sammen: L = B + G
- den første kolonnen inneholder \(2\frac12\) ganger så mange brikker som det er i den tredje kolonnen: R = 2,5 G
R + B + G + L = 20
Vi har ikke nok opplysninger til å sette opp en likning med bare én ukjent. Så her må vi prøve oss litt fram. Siden alle antall i denne oppgaven er hele tall, må R = 2,5G også være et helt tall. Da må antall grønne brikker, G, være et partall. Vi kan for eksempel prøve slik:
| Antall grønne brikker, G | Antall røde, R = 2,5G | Antall blå brikker, B | Antall lilla brikker, B + G | Sum |
| 2 | 5 | 3 | 5 | 15 |
| 4 | 6 | 17 | ||
| 5 | 7 | 19 | ||
| 6 | 8 | 21 | ||
| 4 | 10 | 1 | 5 | 20 (!) |
| 2 | 6 | 22 |
Vi kan også resonnere rundt mulige løsninger:
Hvis vi lar G = 2, blir R = 5. Men siden L = B + G, må L + (B + G) bli et partall. Og et partall + 5 blir aldri 20.
Da må vi prøve med G = 4 som gir R = 10. Da må L + B + G = 10, og altså B + G = L = 5. Og siden G = 4, må B = 1.
Hvis vi lar G = 6, blir R = 15. Da må L + B + G = 5, men det er umulig siden denne summen må bli et partall.
Hvis G = 8, blir R = 20. Da må L + B + G = 0, men det er umulig siden G = 8.
Vi ser at den eneste mulige løsningen er at det er ti røde, en blå, fire grønne og fem lilla brikker.
Lærarrettleiing
Hvorfor arbeide med denne oppgaven?
Vi introduserer uoppstilte likninger ved hjelp av konkreter. Det er en lav inngangsterskel til problemet. Og det å sette opp likninger kan sees på som en direkte «oversettelse» fra det konkrete resultatet til algebraspråket.
Elevene får dessuten erfare at det er vi selv som bestemmer hva den ukjente størrelsen i likningen skal være, og at vi kommer fram til samme løsning uansett hvilken mulig verdi vi lar være ukjent.
Mulig tilnærming
La elevene arbeide i par. Sørg for at alle har tilstrekkelig mange brikker i rødt, blått og grønt, og gi dem oppgavene. Du finner en kopioriginal med oppgavene her.
Følg med på hvordan elevene arbeider og hvilke løsninger de velger. Du må vurdere når det passer å ta en stans og snakke litt sammen i fellesskap.
Noen elever kommer kanskje ikke lenger enn å løse problemet med konkreter. La dem få presentere løsningen sin og be dem forklare hvordan de har tenkt og hvorfor de mener løsningen er riktig.
Kanskje er det nødvendig at du forklarer eller repeterer hva en likning er. Hvis flere synes det er vanskelig å «oversette» fra det konkrete til algebraspråket, kan det passe å stanse litt etter at alle har fått tid til å gruble over oppgave 2. Det er viktig at du som lærer ikke bare viser elevene hvordan de skal sette opp likningene. Like viktig er det at du som lærer sørger for at det er helt tydelig hva som er riktig løsning, etter at dere har sett ulike løsninger og diskutert. Få fram flest mulig forslag fra elevene og ta utgangspunkt i disse når dere diskuterer. La elevene få presentere hva de har gjort. Sørg for at de også forteller hvordan de har tenkt og hvorfor de mener det de har gjort er riktig. Sier de algebraiske uttrykkene det samme som teksten i oppgaven? Hvor mange ukjente er det i likningen? Hvordan går det an å lage en likning med bare én ukjent? Hvilket tall kan være det ukjente tallet? Er det flere tall som kan være det ukjente?
Etter dette kan elevene arbeide videre med oppgavene. Sørg for at de noterer underveis og at de skriver ned alle likningene de lager.
Etter at de fleste har arbeidet seg gjennom oppgavene, kan de få presentere løsningene sine. Ha fokus på
- oversettelse fra det konkrete til algebraspråket
- oppgavene kan løses med flere ulike valg for tallet som skal være det ukjente
- ulike bokstaver kan være symboler for ukjente tall, det kan være x, R, B, G eller andre bokstaver. Det som er avgjørende, er at det er tydelig hva bokstavene står for.
- når likningene er løst, er ikke oppgaven løst. Det må komme en tolkning av det tallet som blir løsning i likningene, og man må formulere et svar på spørsmålet i oppgaven.
Til slutt kan dere få en diskusjon om oppgavene 8 og 9. Kan oppgave 8 løses? Og kan oppgave 9 løses?
Mange har sikkert funnet at oppgave 8 kan løses, men at løsningene ikke blir hele tall. Så i det konkrete tilfellet i oppgave 8, finnes det ingen løsning. Når vi løser med brikker, må løsningen være et helt tall.
Hvis noen er ferdig lenge før de andre, finnes en ekstra utfordring til slutt.
Gode veiledningsspørsmål
Til arbeidet med å løse oppgaven ved hjelp av brikker:
- Kan du legge brikker i tre kolonner slik at forholdet mellom dem blir sli oppgaven sier?
- Hvor mange brikker har du brukt til sammen?
- Hvis du har lagt ut for få brikker, hvor kan du fylle på med flere uten at forhodet mellom dem forandres?
- Hvis du har lagt ut for mange brikker, hvor kan du ta bort brikker uten at forholdet mellom dem forandres?
- Hvordan kan du kontrollere at brikkene du har lagt ut, gir riktig løsning?
Til arbeidet med å sette opp likninger:
- I en likning bruker vi bokstaver på plassene til ukjente tall. Hvilke bokstaver vil du bruke her?
- Hvor mange ukjente tall har du i likningen du setter opp?
- Kan du lage en likning der det bare er én ukjent bokstav?
Til elever som har løst likningene sine:
- Kan du bruke løsningen til å svare på spørsmålet i oppgaven?
Mulig utvidelse
Ekstra utfordring:
Står som siste oppgave.
Bruk 20 brikker til å lage fire kolonner slik at
- den fjerde kolonnen inneholder like mange brikker som den andre og den tredje kolonnen til sammen
- den første kolonnen inneholder \(2\frac12 \) ganger så mange brikker som det er i den tredje kolonnen
Her er det ikke mulig å sette opp en enkelt likning. Den er heller ikke mulig å løse som et likningssett. Mange kan løse oppgaven med konkreter. Hvilke likninger kan vi skrive når vi oversetter oppgaveteksten til algebraspråket? Herfra må vi resonnere eller prøve oss fram. Hvordan kan vi gå fram for å gjøre det videre arbeidet systematisk?
Gode veiledningsspørsmål:
- Ta utgangspunkt i én av kolonnene. Hvilken vil du velge? Hvilken av kolonnene er involvert i begge opplysningene som er gitt i oppgaven?
- Fins det flere enn én løsning? Hvordan kan du være sikker på at det ikke finnes noen flere løsninger enn den du har?
Ressursen er utviklet av Matematikksenteret