Skreddar og skjerf
Aktivitet
Ein skreddar har 6 meter stoff og skal sy skjerf.
a) Til kvart skjerf treng han \(1 \over 2\) meter stoff. Kor mange skjerf kan han sy?
b) Skreddaren skal sy ein annan type skjerf som er slik at det trengst \(1 \over 4\) meter stoff for kvart skjerf. Blir det fleire eller færre skjerf enn i a? Kan du finne ut kor mange skjerf det blir, utan å rekne på nytt? Forklar og grunngi.
c) For ein tredje type skjerf trengst det \(3 \over 4\) meter stoff til kvart skjerf. Blir det fleire eller færre skjerf enn i b? Blir det fleire eller færre skjerf enn i a? Kan du finne ut kor mange skjerf det blir, utan å rekne (heilt) på nytt? Forklar og grunngi.
Tillegsspørsmål:
Kor mykje blir \(10:{5 \over 4}\) og korleis finn du ut det? Kva slags situasjon eller rekneforteljing passar til det reknestykket?
Opplegget er utviklet i forbindelse med MAM (Mestre Ambisiøs Matematikkundervisning)
Løysing
Her går det an å tenkje på mange måtar. Her er nokre forslag:
a) Skreddaren treng \(1 \over 2\) meter per skjerf.
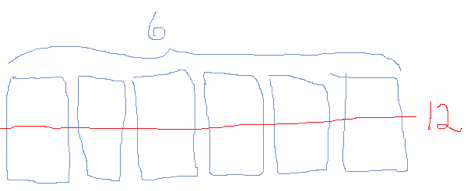
- Ein kan lage ei teikning av 6 meter stoff (som på figuren under), dele alle i to og få 12 bitar på \(1\over 2\) meter.
- \(6: {1 \over 2} =12\)
b) Skreddaren treng \(1 \over 4\) meter per skjerf
- Skjerfa blir kortare, så det er nok stoff til fleire skjerf. Sidan dei nye skjerfa er halvparten så lange som skjerfa i a, blir det dobbelt så mange, altså 24.
- \(6: {1 \over 4}=24\)
c) Skredderen treng \(3 \over 4\) meter per skjerf
- Det blir eit skjerf per meter stoff, med ein rest på \(1 \over 4\) meter. Til saman blir det \(6 \over 4\) meter med rest, som er nok til 2 skjerf på \(3 \over 4\) meter. Så skreddaren får 6 skjerf, pluss dei 2 skjerfa han lagar av «restene». Han får laga 8 skjerf.
- \(6: {3 \over 4}=8\)
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
Føremålet med aktiviteten er at elevane skal sjå på ulike løysingsstrategiar i divisjon (målingsdivisjon) og samanhengen mellom desse strategiane. Oppgåvene legg til rette for at ein kan ha spesielt fokus på det som skjer med svaret når divisor minkar eller aukar med ein gitt faktor. Elevane får utforske divisjon med brøk ved hjelp av ulike representasjonar – teikningar, konkret, tallinje, symbol.
Spørsmåla er knytte til kor mange skjerf skreddaren kan sy. Det er ikkje opplagt for elevane at dei bruker divisjon i denne konteksten. Mange elevar knyter divisjon til ei mengde dei deler likt, med etterfølgjande spørsmål: Kor mykje blir det på kvar? Denne forma for divisjon kallar vi delingsdivisjon. I denne oppgåva er spørsmålet: Kor mange skjerf kan skreddaren sy? Mange elevar vil tenkje at skreddaren får to skjerf på kvar meter. Dei finn løysinga, 12 skjerf, ved å multiplisere 6 med 2. Be elevane reflektere rundt rekningsarten dei vel, og kva reknestykket fortel. Kva representerer talet 6? Kva representerer talet 2? Kvar er talet \(1 \over 2\)?
Mogleg tilnærming
Oppgåve a kan presenterast munnleg for elevane. Dei arbeider parvis og uttrykkjer løysingsforslaga sine skriftleg. Kan oppgåva løysast på fleire måtar? Ulike løysingsstrategiar bør du løfte fram i ein felles diskusjon. Du kan notere dei ulike framgangsmåtane på tavla. La elevane argumentere for svara sine.
Presenter også dei to andre oppgåvene munnleg for elevane. La elevane prøve å finne løysingar utan å begynne heilt på nytt igjen, og grunngi desse løysingane. Dei arbeider framleis parvis og skriv forslaga på store ark eller plakatar, slik at løysingane kan presenterast for dei andre i klassen. Elevane forklarer og grunngir. Oppfordre dei til å bruke ulike representasjonar.
Observerer arbeidet og vel rekkjefølgja på presentasjonane. Diskusjonen og oppsummeringa kan etter kvart fokusere på rekneoperasjonane og dei reknestykka som gir svar på problemstillingane. Å vurdere og diskutere det at svara blir større når vi bruker divisjon, er viktig. Mange elevar trur jo at multiplikasjon gir større tal, og at divisjon gir mindre tal.
Gode rettleiingsspørsmål
- Kva vil skreddaren gjere med tøystykket på 6 meter?
- Korleis vil de forklare framgangsmåten dykkar for dei andre i klassen?
- Kan de vise løysinga ved hjelp av andre representasjonar (teikningar, konkret, tallinje, symbol)?
- Ser de nokon samanheng mellom dei ulike oppgåvene?
- Kva for ein rekningsart passar til kvar oppgåve?
- Kva for eit reknestykke beskriv situasjonen? Kva fortel reknestykket?
- Korleis ville det bli dersom skreddaren brukte 3 meter per skjerf? Kva for eit reknestykke ville passe til oppgåva? (3 går to gonger opp i 6.)
- Korleis ville det bli dersom han brukte 1 meter per skjerf? (1 går seks gonger opp i 6.)
- Korleis ville reknestykket bli dersom han trong ½ meter per skjerf? Forklar og grunngi. (\(1 \over 2\) går 12 gonger opp i 6.)
Mogleg støtte
Somme vil kunne ha nytte av måleband og eventuelt hyssing i arbeidet med denne oppgåva. Teikning vil også vere ei god støtte i arbeidet. Dersom nokon strevar med å sjå at det er divisjon dei driv med, kan det vere ein god idé å gå vegen via divisjon med heiltal. Du kan spørje elevane korleis reknestykket blir dersom skreddaren syr skjerf som er 2 eller 3 meter lange. Då kan det også vere lettare å overføre strategien til skjerfa som skal vere \(1 \over 2\) meter lange.
Ressursen er utviklet av Matematikksenteret