Utforsking av rotasjon
Aktivitet
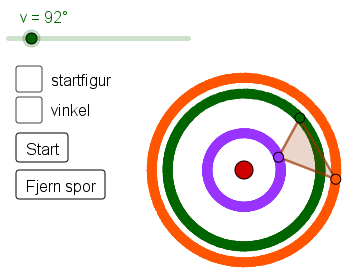
I GeoGebra-appleten nedanfor kan du bevege på glidaren for å rotere figuren rundt det rødde punktet. Figuren kan også roterast automatisk ved å trykkje på "Start"-knappen. Avkryssingsboksen "startfigur" avgjer om den originale figuren blir vist eller ikkje.
Prøv deg fram i appleten og noter nokon tankar om:
- Kvifor blir det teikna sirklar?
- Kva betyr tala på glidaren?
- Kvar ligger figuren viss glidaren står på \(90^\circ\) eller \(180^\circ\)?
- Kva skjer om vi roterer med \(360^\circ\), \(540^\circ\) eller \(720^\circ\)?
- Kvar er vinkelen som GeoGebra måler?
- Vinkelen aukar når vi dreg glidaren mot høgre, men kvifor startar han på nytt etter \(360^\circ\)?
Etter at de har diskutert spørsmåla ovanfor i klassen, arbeider du vidare med å utforske rotasjonseigenskapane til likesida mangekantar. Du kan bruke GeoGebra-appleten nedanfor på same måte som den førre, og du kan i tillegg endre kor mange kantar mangekanten skal ha.
- Må du alltid rotere \(360^\circ\) for at den roterte figuren skal dekkje originalfiguren? Eksperimenter ved å flytte rotasjonssenteret utanfor, på, og inni figuren.
-
Kva er det minste talet på grader du kan rotere ein likesida femkant, eit kvadrat og ein likesida trekant slik at den roterte figuren dekkjer originalfiguren?
-
Skriv ei forklaring på kvifor du meiner at løysinga er rett.
-
Kva er minste talet på grader for ein likesida sekskant?
-
Kva er minste talet på grader for ein n-kant?
-
Test hypotesen ved utprøving.
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
Målet med oppgåva er at elevane skal bli kjent med eigenskapane til rotasjon. Oppgåva gir elevane høve til å oppdage kva som skjer når ein figur blir rotert. Elevane skal utvikle forståing for kva som skjer når vi roterer eit objekt, kva som kjenneteiknar eit rotasjonssymmetrisk objekt, korleis dei finn rotasjonssenteret til ein slik figur, kva rotasjonsvinkel er, og korleis dei finn rotasjonsvinkelen.
Mogleg tilnærming
Om det er lenge sidan elevane har arbeidet med eigenskapane til todimensjonale figurar (vinklar, kantar, hjørne), kan det vere formålstenleg med ei oppfrisking om dette før du introduserer problema i denne oppgåva. Om du ikkje vil at elevane skal bruke den ferdige GeoGebra-appleten med mangekantar, men at dei heller skal lage figurane i GeoGebra sjølv, treng dei også å kunne teikne regulære mangkantar, måle vinklar og laga glidarar i GeoGebra. Oppgåva legg godt til rette for verktøyopplæring i GeoGebra, men du må påberegne noko tid til dette i tillegg til arbeidet med oppgåva.
Start med å vise elevane den øvste GeoGebra-appleten. Animer glidaren slik at trekanten roterer rundt det raude punktet, du kan anten bruke glidaren for å endre rotasjonsvinkelen, eller trykkje på Start-knappen for å animere glidaren. Du kan velje om originalfiguren (startfigur) og rotasjonsvinkelen skal visast, i tillegg til den roterte figuren. Det er sett sporing på hjørna til trekanten som blir rotert, slik at elevane kan følgje rørsla til punkta. Det kan vere lurt å stoppe animasjonen etter kvart, endre originalfiguren og animere glidaren på nytt, slik at elevane ser at punkta bevegar seg i ein sirkel rundt rotasjonspunktet kvar gong. La gjerne elevane bestemme kva som skal endrast før animasjonen startar på nytt, og be dei føresjå kva som kjem til å skje. Gi elevane litt tid til å utforske figuren på eigenhand, men pass på at dei undersøkjer tilfelle der rotasjonssenteret er utanfor, på og innanfor figuren.
Diskuter i heilklasse kva elevane har sett. Kvifor blir det teikna sirklar? Kva betyr tala på glidaren? Kvar ligg figuren viss glidaren står på … ? Her kan det også vere lurt å spørje om kva som skjer når ein roterer med …. Desse vinklane er godt kjende for elevar som liker snøbrett eller rullebrett, noko som gjer det lettare å knyte rotasjon til noko dei kan frå før.
Etter klassediskusjonen ber du elevane arbeide vidare i par eller små grupper med å utforske likesida (regulære) mangekantar i GeoGebra. Elevane skal finne ut kor mange grader dei må rotere mangekanten for å få den roterte figuren til å dekkje originalfiguren. Må dei alltid rotere …, eller er det mogleg å rotere med ein mindre vinkel? Elevane vil oppdage at plasseringa av rotasjonssenteret er avgjerande for at dei skal kunne dekkje originalfiguren ved å rotere med ein vinkel som er mindre enn ….
Om du vil at elevane sjølv skal lage figurane i eit tomt Geogebra-vindauge, kan det vere lurt å be dei lukke nettsida som inneheld den ferdige appleten. Du kan skrive ut oppgåvearket som ligg i menyen til venstre, og dele ut til elevane.
Det er viktig at elevane får prøve (og feile) utan at vi kjem med løysingane. Slik blir dei både betre problemløysare, samtidig som verktøykunnskapen i GeoGebra blir utvikla.
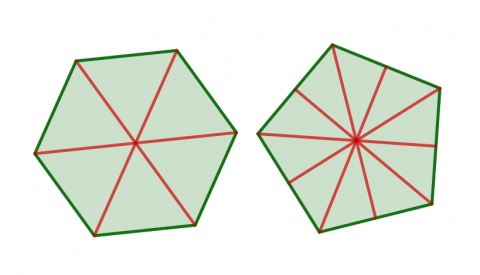
Elevane løyser problemet ved utforsking. Først må dei finne ut kva betydning plasseringa av rotasjonssenteret har, og kva som skjer når dei roterer med ulike vinklar. Deretter må dei diskutere og resonnere seg fram til kvifor akkurat desse vinklane fungerer når rotasjonssenteret er plassert i midten av mangekanten. Etter å ha argumentert for løysingane sine, skal dei finne ein generell regel som gjeld for alle likesida mangekantar når rotasjonssenteret er plassert i midten av figuren. Elevane vil også oppdage at det er enklare å finne midtpunktet viss talet på sider i mangekanten er eit partal enn eit oddetal (sjå biletet nedanfor). Kvifor er det slik?
Som oppsummering kan elevane vise fram korleis dei har tenkt, og kva for nokre matematiske samanhengar dei har funne. Vel ut elevar som skal presentere arbeidet sitt basert på observasjonane som er gjorde undervegs. Det er viktig å velje ut elevar som har brukt ulike løysingsmetodar. Pass samtidig på å forklare og ta i bruk relevante matematiske omgrep som rotasjonssymmetrisk, rotasjonssentrum og rotasjonsvinkel.
Mogleg utviding
Oppgåvene Rotasjonsmønster og Trekanta hjul.
Ressursen er utviklet av Matematikksenteret