Læreplankoblet

Steinar på stranda

Stikkord: Rom og form Tallforståelse

Aktivitet

Sjå for deg at du går på ei fin sandstrand, så får du øye på nokre små steinar her og der. Du plukkar opp fire steinar og legg dei slik at dei dannar form som eit kvadrat. Arealet av kvadratet er 1 kvadrat-ett-eller-annet, kanskje 1 kvadratmeter, 1 kvadratcentimeter, 1 kvadratfinger, 1 kvadratsko, eller liknande.

Vi kan seie at kvadratet du har lagt, skal ha areal 1.

Thumbnail

Ved å leggje til to nye steinar kan vi doble arealet frå 1 til 2, slik:

Thumbnail

Regelen som utviklar seg her, er å ikkje røre steinane som allereie er lagde, og leggje til så få steinar som mogleg for å doble det førre arealet. Det er berre lov å leggje rektangel.

Så viss vi held fram, kan vi leggje til tre nye steinar for å doble arealet frå 2 til 4, slik:

Thumbnail

Her trong vi tre nye steinar.

Det er også mogleg å doble arealet frå 2 til 4 ved å gjere slik:

Thumbnail

Her brukte vi fire steinar. Ei slik løysing følgjer ikkje regelen om å bruke så få steinar som mogleg, så denne løysinga er ikkje gyldig.

Nummer 6 vil sjå slik ut:

Thumbnail
Thumbnail

Hugs! Ikkje flytt på steinane som er lagde, og doble det førre arealet ved å leggje til så få steinar som mogleg kvar gong. 

No er det din tur!

Sjå på formene du har laga. Legg du merke til noko spesielt?

Lag nokon fleire. Kor mange kan du lage? Du vil kanskje gå tom for teljebrikker, perler eller kva du enn bruker.

Utforsk dette:

  • Kor mange ekstra steinar må du leggje til kvar gong? Det startar slik: 2, 3, 6 …
  • Kor mange steinar er det rundt den ytste kanten? Det startar slik: 4, 6, 8 …
  • Kor stort er arealet? Det startar slik: 1, 2, 4 …
  • Kor mange steinar er det inni rektangla? Det startar slik: 0, 0, 1, 3, 9 …
  • Kan du finne på nokon spørsmål sjølv? 
  • Spør deg sjølv: «Kva vil skje viss ..?»

Forsøk å svare på desse spørsmåla og andre spørsmål du kjem på sjølv, og notar resultatet i eit skjema.

Starthjelp

  • Bruk konkretar til hjelp, til dømes teljebrikker og eit ruteark.

  • Kan du lage eit rektangel med berre éin stein til? Kva med to? Tre?

  • Har du forsikra deg om at kvart rektangel har dobbelt så stort areal som det førre?

  • Korleis held du oversikt over det du har gjort?

Løysing

 

Nummer

Form

Mengd steinar

Areal

Omkrets

1

Kvadrat

2 · 2 = 4

1 cm2

4 cm

2

Rektangel

2 · 3 = 6

2 cm2

6 cm

3

Kvadrat

3 · 3 = 9

4 cm2

8 cm

4

Rektangel

3 · 5 = 15

8 cm2

12 cm

5

Kvadrat

5 · 5 = 25

16 cm2

16 cm

6

Rektangel

5 · 9 = 45

32 cm2

24 cm

7

Kvadrat

9 · 9 = 81

64 cm2

32 cm

8

Rektangel

9 · 17 = 153

128 cm2

48 cm

 

Lærarrettleiing

Kvifor arbeide med denne oppgåva?

Denne aktiviteten har ei utforskande tilnærming der elevane må ta omsyn til både rom og form. I tillegg legg aktiviteten til rette for at elevane kan utvikle talforståinga si. Aktiviteten kan vere krevjande i den forstand at dei ofte må jobbe litt for å komme til svaret. Det gir deg som lærer eit fint høve til å teste uthaldet til elevane og utvikle han.

Mogleg tilnærming

Ein fin måte å starte denne aktiviteten på er å samle heile klassen og lage dei to eller tre første areala saman. Det kan vere nyttig for elevane å ha ruteark tilgjengeleg, gjerne med utheva prikkar, og små teljebrikker som kan representere steinane. Eit interaktivt geobrett kan brukast på smartboard til å vise og til å dele ideane til elevane. 

Etter at elevane har arbeidd i par ei stund, og undersøkt ulike talmønster som oppstår, kan du stille nokre av spørsmåla under for å invitere elevane til sjølv å stille og utforske deira eigne spørsmål. Oppmuntre dei til å notere og halde #styr på oppdagingane sine på den måten dei sjølv meiner er best.

Gode rettleiingsspørsmål

  • Kva tel du? (Nokre gonger kan det oppstå forvirring når elevane skal telje steinar eller talet på mellomrom mellom steinane, spesielt når dei skal telje sidene.)

  • Har dette rektangelet eller kvadratet dobbelt så stort areal som det førre?

  • Korleis held du oversikt over det du har gjort?

Mogleg utviding

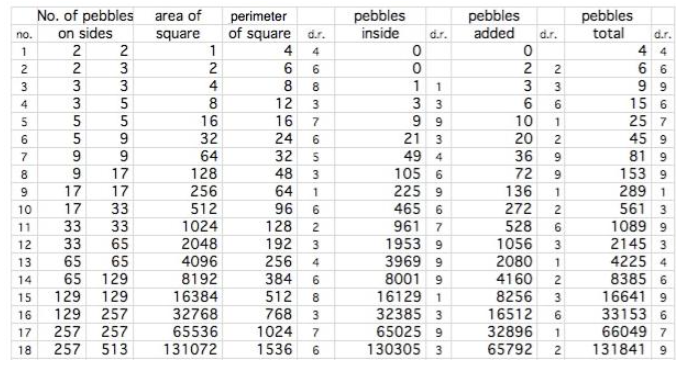
Nokre elevar vel å halde oversikt over oppdagingane sine ved å lage ein tabell eller bruke eit rekneark. Når dei noterer resultata systematisk, har dei høve til å utforske vidare. 

Her er eit døme:

Thumbnail

d.r.= digital root (sifferrot).

Døme: Sifferroten av 247 = 4, fordi 2 + 4 + 7 = 13 og 1 + 3 = 4)

Ressursen er utviklet av NRICH

8